题目内容
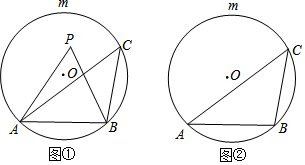
15.已知AB是⊙O的一条弦,点C是优弧$\widehat{AmB}$上一点.(1)如图①,若点P是弦AB与$\widehat{AmB}$所围成的弓形区域(不含弦AB与$\widehat{AmB}$)内一点.求证:∠APB>∠ACB;
(2)如图①,若点P在弦AB上方,且满足∠APB=∠ACB,则点P在$\widehat{AmB}$上吗?为什么?
(3)请在图②中直接用阴影部分表示出在弦AB与$\widehat{AmB}$所围成的弓形区域内满足∠ACB<∠APB<2∠ACB的点P所在的范围.
分析 (1)根据题意画出相应的图形,根据三角形的外角大于任何一个和它不相邻的内角,可以证明结论成立,本题得以解决;
(2)点P在$\widehat{AmB}$上,利用(1)的结论和同(1)的方法即可得出结论;
(3)根据题意和第(1)问,可以画出满足∠ACB<∠APB<2∠ACB的点P所在的范围,本题得以解决
解答 (1)证明:如下图②所示,
延长AP交⊙O于点Q,连接BQ.
则∠PQB=∠ACB,
∵∠APB为△PQB的一个外角,
∴∠APB>∠PQB,
即∠APB>∠ACB;
(2)解:点P在$\widehat{AmB}$上,
理由:由(1)知,点P是弦AB与$\widehat{AmB}$所围成的弓形区域(不含弦AB与$\widehat{AmB}$)内一点,∠APB>∠ACB,
同(1)的方法,点P在弦AB上半部分时,利用三角形的外角,得,∠APB<∠ACB,
∴点P在$\widehat{AmB}$上,
(3)解:
连接AO,BO,延长BO,在BO的延长线上取一点P连接AP,
∵∠AOB是△APO的外角,
∴∠AOB>∠APB,
∵∠AOB是在⊙O中劣弧AB所对的圆心角,∠ACB是⊙O中劣弧AB所对的圆周角,
∴∠AOB=2∠ACB,
∴点P所在的范围如下图③所示,
点评 此题是圆的综合题,主要考查了三角形的外角的性质,同弧所对的圆心角和圆周角的关系,解本题的关键是作出辅助线.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
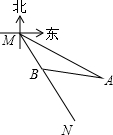 如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区.取MN上另一点B,测得∠ABN=45°.已知MB=400m,如果不改变方向,输水线路是否会穿过居民区?说明理由.
如图,已知MN表示某引水工程的一段设计路线,从M到N的走向为南偏东30°,在M的南偏东60°方向上有一点A,以A为圆心,500m为半径的圆形区域为居民区.取MN上另一点B,测得∠ABN=45°.已知MB=400m,如果不改变方向,输水线路是否会穿过居民区?说明理由.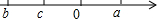 (1)实数a,b,c在数轴上的对应点如图所示,化简$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|.
(1)实数a,b,c在数轴上的对应点如图所示,化简$\root{3}{{a}^{3}}$+|a+b|-$\sqrt{{c}^{2}}$-|b-c|.