题目内容
3.如图(a),直角梯形ABCD,∠B=90°,DC∥AB,动点P从B点出发,以每秒2个单位长度,由B-C-D-A沿边运动,设点P运动的时间为x秒,△PAB的面积为y,如果关于x的函数y的图象如图(b),则函数y的最大值为72.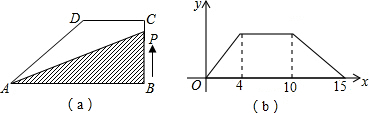
分析 根据图象信息,求出梯形各边的长度,确定函数取最大值时,点P的运动时间,然后根据三角形面积公式求出面积即可.
解答  解:过E作DE⊥AB,交AB于点E,可得BE=CD,DE=BC,
解:过E作DE⊥AB,交AB于点E,可得BE=CD,DE=BC,
根据图(b)中的信息得到BC=8,DC=12,AD=10,
在Rt△ADE中,AD=10,DE=8,
由勾股定理,AE=6,
则AB=18,
故△PAB的面积的最大值为:$\frac{1}{2}$×18×8=72.
故答案为:72.
点评 本题考查的是动点问题,读懂函数图象、从中获取正确的信息是解题的关键,通过图象和题意,确定函数取最大值时自变量x的取值范围是重点.

练习册系列答案
相关题目
10.已知直线y=x-3与函数y=$\frac{2}{x}$的图象相交于点(a,b),则a2+b2的值是( )
| A. | 13 | B. | 11 | C. | 7 | D. | 5 |

 有意义,则x的取值范围是 .
有意义,则x的取值范围是 . 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?
我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?