Question

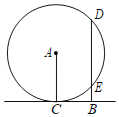
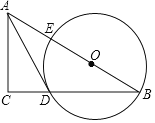
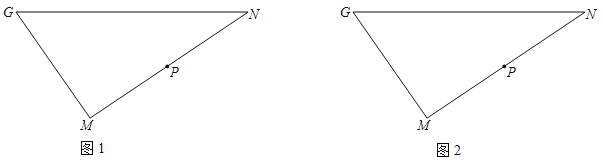
【题目】如图1，在Rt△GMN中，∠M＝90°，P为MN的中点

（1）将线段MP绕着点M逆时针旋转60°得到线段MQ，点P的对应点为Q，若点Q刚好落在GN上，

①在图1中画出示意图；

②试问：以线段MQ为直径的圆是否与GN相切？请说明理由；

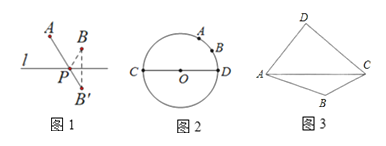
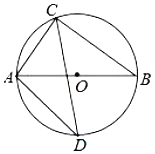
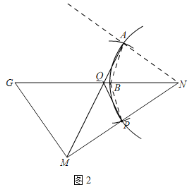
（2）如图2，用直尺和圆规在GN边上求作点Q，使得∠GQM＝∠PQN．（保留作图痕迹，不要求写作法）

Answer 1

【答案】（1）①见解析，②以MQ为直径的圆与GN相切，理由见解析；（2）见解析

【解析】

（1）①根据旋转直接画出图形即可；

②先判得出是等边三角形，进而求出，再判得出，进而求出，判断出，即可得出结论；

（2）先作出，再截出，连接AM交GN于Q，即可得出结论.

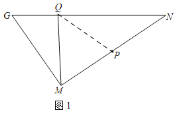
（1）①根据旋转直接画图，结果如图1所示：

②以MQ为直径的圆与GN相切，理由如下：

如图1，连接PQ

由旋转的性质可知，

是等边三角形

∵点P是MN的中点

则以MQ为直径的圆与GN相切；

（2）如图2，先作出，再截出，连接AM交GN于Q，点Q为所求作的点.理由如下：

连接AB、PB

由作图知，

，即

连接AM交GN于点Q，连接PQ

（对顶角相等）

.