题目内容
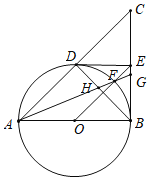
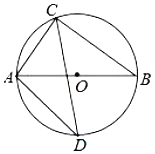
【题目】如图,![]() 是
是![]() 的直径,
的直径,![]() 、
、![]() 为
为![]() 上的点,若
上的点,若![]() ,
,![]() ,若
,若![]() 平分
平分![]() ,则
,则![]() 长为( )
长为( )
A.10B.7C.![]() D.
D.![]()
【答案】D
【解析】
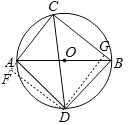
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.由Rt△AFD≌Rt△BGD(HL),推出AF=BG,由Rt△CDF≌Rt△CDG(HL),推出CF=CG,由△CDF是等腰直角三角形,得CD=![]() CF,求出CF即可解决问题.
CF,求出CF即可解决问题.
作DF⊥CA,垂足F在CA的延长线上,作DG⊥CB于点G,连接DA,DB.
∵∠AFD=∠BGD=90°,
在Rt△ADF和Rt△BDG,
![]() ,
,
∴Rt△AFD≌Rt△BGD(HL),
∴AF=BG.
同理:Rt△CDF≌Rt△CDG(HL),
∴CF=CG.
∵AB是直径,
∴∠ACB=90°,
∵AC=6,BC=8,
∴AB=![]() ,
,
∴6+AF=8-AF,
∴AF=1,
∴CF=7,
∵CD平分∠ACB,
∴∠ACD=45°,
∵△CDF是等腰直角三角形,
∴CD=![]() CF=7
CF=7![]() .
.
故选D.

练习册系列答案
相关题目
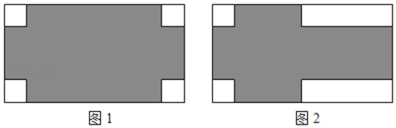
【题目】某公司对自家办公大楼一块![]() 米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形
米的正方形墙面进行了如图所示的设计装修(四周阴影部分是八个全等的矩形,用材料甲装修;中心区是正方形![]() ,用材料乙装修). 两种材料的成本如下表:
,用材料乙装修). 两种材料的成本如下表:

材料 | 甲 | 乙 |
价格(元/米2) | 550 | 500 |
设矩形的较短边![]() 的长为
的长为![]() 米,装修材料的总费用为
米,装修材料的总费用为![]() 元.
元.
(1)计算中心区的边![]() 的长(用含
的长(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 关于
关于![]() 的函数解析式;
的函数解析式;
(3)当中心区的边长![]() 不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.
不小于2米时,预备材料的购买资金32000元够用吗?请利用函数的增减性来说明理由.