Question

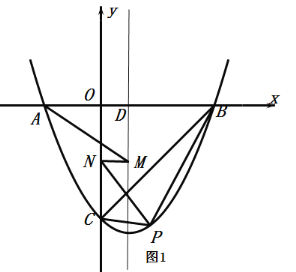
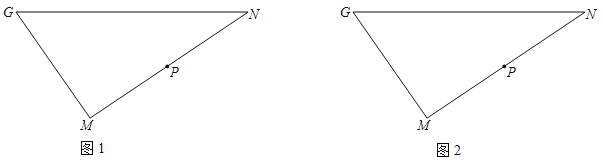
【题目】在平面直角坐标系中，直线分别与，轴交于，两点，点在线段上，抛物线经过，两点，且与轴交于另一点.

（1）求点的坐标（用只含，的代数式表示）；

（2）当时，若点，均在抛物线上，且，求实数的取值范围；

（3）当时，函数有最小值，求的值.

Answer 1

【答案】（1）；（2），；（3）或.

【解析】

（1）在一次函数中求点A,B的坐标，然后将点C,A坐标代入二次函数解析式，求得，令y=0，解方程求点D的坐标；（2）由C点坐标确定m的取值范围，结合抛物线的对称性，结合函数增减性分析n的取值范围；（3）利用顶点纵坐标公式求得函数最小值，然后分情况讨论：当点在点的右侧时或做测时，分别求解.

解：（1）∵直线分别与，轴交于，两点，

∴，.

∵抛物线过点和点，

∴.

∴.

令，得.

解得，.

∴.

（2）∵点在线段上，

∴.

∵，

∴，.

∴抛物线的对称轴是直线.

在抛物线上取点，使点与点关于直线对称.

由得.

∵点在抛物线上，且，

∴由函数增减性，得，.

（3）∵函数有最小值，

∴.

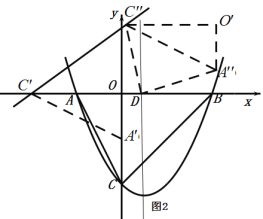
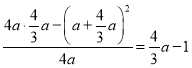①当点在点的右侧时，得，解得.

∴，解得，.

②当点在点的左侧时，得，解得.

∴.

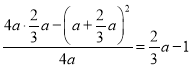解得：，.

综上所述，或.