题目内容
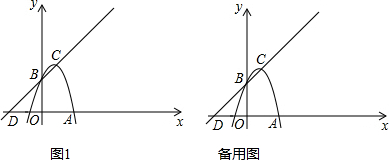
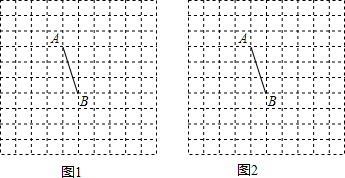
9.如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=$\sqrt{2}$;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+$\sqrt{2}$;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3,此时AP3=2+$\sqrt{2}$;…,按此规律继续旋转,直至得到点P2015为止.则AP2015=1343+672$\sqrt{2}$.
分析 由等腰直角三角形的性质和已知条件得出AP1=$\sqrt{2}$,AP2=1+$\sqrt{2}$,AP3=2+$\sqrt{2}$;AP4=2+2$\sqrt{2}$;AP5=3+2$\sqrt{2}$;AP6=4+2$\sqrt{2}$;AP7=4+3$\sqrt{2}$;AP8=5+3$\sqrt{2}$;AP9=6+3$\sqrt{2}$;每三个一组,由于2013=3×671,得出AP2013,即可得出结果.
解答 解:AP1=$\sqrt{2}$,AP2=1+$\sqrt{2}$,AP3=2+$\sqrt{2}$;
AP4=2+2$\sqrt{2}$;AP5=3+2$\sqrt{2}$;AP6=4+2$\sqrt{2}$;
AP7=4+3$\sqrt{2}$;AP8=5+3$\sqrt{2}$;AP9=6+3$\sqrt{2}$;
∵2015=3×671+2,
∴AP2013=(2013-671)+671$\sqrt{2}$=1342+671$\sqrt{2}$,
∴AP2014=1342+671$\sqrt{2}$+$\sqrt{2}$=1342+672$\sqrt{2}$,
∴AP2015=1342+672$\sqrt{2}$+1=1343+672$\sqrt{2}$.
故答案为:1343+672$\sqrt{2}$.
点评 本题考查了旋转的性质:旋转前后两图形全等;对应点到旋转中心的距离相等;根据题意得出规律是解决问题的关键.

练习册系列答案
相关题目
19.方程(x+4)(x-1)=0的解是( )
| A. | x=1 | B. | x=-4 | C. | x1=-4,x2=1 | D. | x1=4,x2=-1 |
4.下面四个数中比-3小的数是( )
| A. | 2 | B. | 0 | C. | -2 | D. | -4 |
1.如图,AD、BE是△ABC的两条中线,则S△EDC:S△ABD等于( )
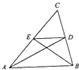

| A. | 1:2 | B. | 2:3 | C. | 1:3 | D. | 1:4 |
19.国家统计局发布的数据显示,初步核算,一季度国内生产总值约159000亿元,按可比价格计算,同比增长6.7%,数据159000亿用科学记数法可表示为( )
| A. | 1.59×108 | B. | 15.9×1012 | C. | 1.59×1013 | D. | 1.59×1014 |
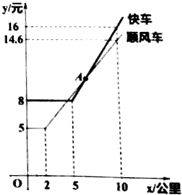 随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法:
随着互联网的发展,互联网消费逐渐深入人们生活,如图是“滴滴顺风车”与“滴滴快车”的行驶里程x(公里)与计费y(元)之间的函数关系图象,下列说法: