题目内容
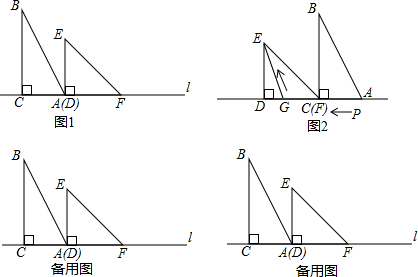
4.有两个直角三角形,在△ABC中,∠ACB=90°,AC=3,BC=6,在△DEF中,∠FDE=90°,DE=DF=4.将这两个直角三角形按图1所示位置摆放,其中直角边AC与DF在同一直线l上,且点A与点D重合.现固定△DEF,将△ABC以每秒1个单位长度的速度在l上向右平移,当点C与点F重合时运动停止.设平移时间为t秒.(1)当t为2秒时,AB边恰好经过点E;当t为7秒时,运动停止;
(2)在△ABC平移过程中,设△ABC与△DEF重叠部分的面积为S,请直接写出S与t的函数关系式,并写出t的取值范围;
(3)当△ABC停止运动后,如图2,G为线段DA上一点,若一动点P从点A出发,先沿AG方向运动,到达点G后再沿斜坡GE方向运动到达点E,若该动点P在线段DA上运动的速度是它在斜坡GE上运动速度的2倍,试确定斜坡GE的坡度,使得该动点从点A运动到点E所用的时间最短.(要求,简述确定点G位置的方法,但不要求证明.)
分析 (1)过E作EH∥AB,交l于H,则DH为AB边移动的距离,利用△AHE∽△CAB,求出AH的长,即可求出AB的运动时间;当C与F重合时,C点运动的路为CF,即可求出时间t;
(2)利用相似三角形的知识可分时间段求出S与t之间的函数关系式;
(3)在l的下方作∠DAM=30°,再过点E作EN⊥AM于N,交AD于G,此时运动时间最短.
解答 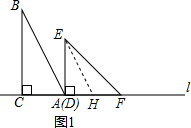 解:(1)如图1所示,过E作EH∥AB,交l于H,
解:(1)如图1所示,过E作EH∥AB,交l于H,
∵BC⊥AC,ED⊥AC,
∴∠BCA=∠EDH=90°.
∵EH∥AB,
∴∠EHD=∠BAC,
∴△AHE∽△CAB,
∴$\frac{DH}{CA}$=$\frac{ED}{BC}$,即$\frac{DH}{3}$=$\frac{4}{6}$,解得DH=2,
∴当t为2秒时,AB边恰好经过点E.
∵AC=3,DF=4,
∴当t=3+4=7秒时,运动停止.
故答案为:2,7;
(2)如图2,当0<t≤2时,
∵BC⊥AC,GD⊥AC,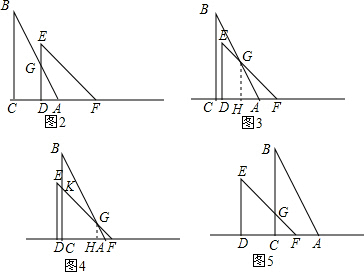
∴$\frac{GD}{BC}$=$\frac{AD}{AC}$,即$\frac{GD}{6}$=$\frac{t}{3}$,解得GD=2t,
∴S=$\frac{1}{2}$AD•GD=$\frac{1}{2}$×t×2t=t2;
如图3所示,当2<t≤3时,
同理可得△GHA∽△BCA,
∴$\frac{GH}{BC}$=$\frac{AH}{AC}$,即$\frac{AH+4-t}{6}$=$\frac{AH}{3}$,解得AH=4-t,
∴GH=2(4-t)=8-2t,
∴S=$\frac{1}{2}$DF•DE-$\frac{1}{2}$AF•GH=$\frac{1}{2}$×4×4-$\frac{1}{2}$×(4-t)(8-2t)=-t2+8t-8;
如图4所示,当3<t≤4时,过点G作GH⊥AD,则AF=4-t,
同上可得GH=2(4-t),
∵△DEF是等腰直角三角形,
∴△CKF也是等腰直角三角形,
∴CK=CF=AC+AF=3+(4-t)=7-t,
∴S=S△DKF-S△AFG=$\frac{1}{2}$(7-t)2-(4-t)2=-$\frac{{t}^{2}}{2}$+t+$\frac{17}{2}$;
如图5所示,当4<t≤7时,S=S△CFG=$\frac{1}{2}$(7-t)2.
综上所示,S=$\left\{\begin{array}{l}{t}^{2}(0<t≤2)\\-{t}^{2}+8t-8(2<t≤3)\\-\frac{{t}^{2}}{2}+t+\frac{17}{2}(3<t≤4)&\\ \frac{1}{2}{(7-t)}^{2}(4<t<7)&\end{array}\right.$;
(3)如图6,在l的下方作∠DAM=30°,再过点E作EN⊥AM于点N,交AD于点G,此时运动时间最短,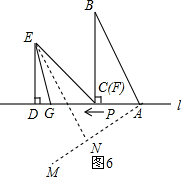
∴∠AGN=60°,
∴∠EGD=60°,
∴i=$\sqrt{3}$.
设点P在斜坡上运动的速度是v,则在AD上运动的速度是2v,从A到E运动的时间为T,则T=$\frac{AG}{2v}$+$\frac{EG}{v}$=$\frac{\frac{AG}{2}}{v}$+$\frac{EG}{v}$=$\frac{1}{v}$($\frac{AG}{2}$+EG),
∴作∠DAM=30°,过点E作EN⊥AM,
∴GN=$\frac{AG}{2}$,
∴当EG+GN最小时,时间最短,即点E、G、N共线时,时间最短.
点评 本题考查的是几何变换综合题,在解答(2)时要注意画出图形,利用数形结合求解.

 阅读快车系列答案
阅读快车系列答案| A. | 6×106 | B. | 6×107 | C. | 6×108 | D. | 60×106 |
| A. | 56940名考生 | B. | 所抽取的2000名考生的数学成绩 | ||
| C. | 56940名考生的数学成绩 | D. | 所抽取的2000名考生 |
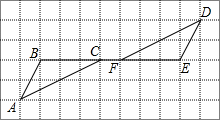 如图,AB∥DE,AB=DE,BF=EC.
如图,AB∥DE,AB=DE,BF=EC.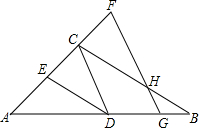 如图,已知∠ADE=∠B,∠EDC+∠CHG=180°,那么∠ECD=∠F吗?为什么?
如图,已知∠ADE=∠B,∠EDC+∠CHG=180°,那么∠ECD=∠F吗?为什么?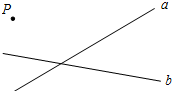 (1)在图中画出表示点P到直线a距离的线段PM;
(1)在图中画出表示点P到直线a距离的线段PM;