题目内容
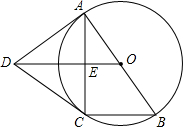 如图,AB是⊙O直径,AC是弦,OE⊥AC于点E,过A作⊙O的切线DA,DA与OE的延长线交于点D,连接DC,BC.
如图,AB是⊙O直径,AC是弦,OE⊥AC于点E,过A作⊙O的切线DA,DA与OE的延长线交于点D,连接DC,BC.(1)填空:OE与BC的位置关系是
(2)求证:DC是⊙O的切线.
考点:切线的判定
专题:
分析:(1)由OE⊥AC,易得OE是△ABC的中位线,则可求得OE与BC的位置与数量关系;
(2)首先连接OC,由OE⊥AC,易得∠AOD=∠COD,则可证得△DAO≌△DCO,继而证得∠DCO=∠DAO=90°,即可得DC是⊙O的切线.
(2)首先连接OC,由OE⊥AC,易得∠AOD=∠COD,则可证得△DAO≌△DCO,继而证得∠DCO=∠DAO=90°,即可得DC是⊙O的切线.
解答:解:(1)∵OE⊥AC,
∴AE=CE,
∵OA=OB,
∴OE是△ABC的中位线,
∴OE∥BC,OE=
BC;
故答案为:OE∥BC,OE=
BC;
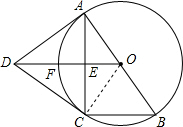 (2)连接OC,设OD与⊙O交于点F,
(2)连接OC,设OD与⊙O交于点F,
∵DA是⊙O的切线,
∴OA⊥AD,
即∠DAO=90°,
∵OE⊥AC,
∴
=
,
∴∠AOD=∠COD,
在△DAO和△DCO中,
,
∴△DAO≌△DCO(SAS),
∴∠DCO=∠DAO=90°,
∴DC是⊙O的切线.
∴AE=CE,
∵OA=OB,
∴OE是△ABC的中位线,
∴OE∥BC,OE=
| 1 |
| 2 |
故答案为:OE∥BC,OE=
| 1 |
| 2 |
 (2)连接OC,设OD与⊙O交于点F,
(2)连接OC,设OD与⊙O交于点F,∵DA是⊙O的切线,
∴OA⊥AD,
即∠DAO=90°,
∵OE⊥AC,
∴
 |
| AF |
 |
| FC |
∴∠AOD=∠COD,
在△DAO和△DCO中,
|
∴△DAO≌△DCO(SAS),
∴∠DCO=∠DAO=90°,
∴DC是⊙O的切线.
点评:此题考查了切线的性质与判定、三角形中位线的性质以及全等三角形的判定与性质.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
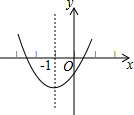 已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)4a-2b+c<0.则正确的结论有( )
已知二次函数y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,给出下列结论:(1)b2>4ac;(2)abc>0;(3)2a+b=0;(4)a+b+c>0;(5)4a-2b+c<0.则正确的结论有( )| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,在Rt△ABC,∠C=90°,AC=8,BC=6,则sinB的值等于( )
如图,在Rt△ABC,∠C=90°,AC=8,BC=6,则sinB的值等于( )A、
| ||
B、
| ||
C、
| ||
D、
|
某校原来有学生x人,本学期开学时,七年级招学生n人,九年级毕业学生(n-3)人,则该校现有学生人数是(单位:人)( )
| A、x+3 | B、x-3 |
| C、x+2n-3 | D、2n-3 |
 如图,AB=AC,则数轴上点C所表示的数为( )
如图,AB=AC,则数轴上点C所表示的数为( )A、
| ||
B、-
| ||
C、-
| ||
D、
|
将△ABC的三个顶点坐标的横坐标保持不变,纵坐标都乘以-1,则所得图形与原图形的关系是( )
| A、关于y轴对称 |
| B、关于x轴对称 |
| C、将原图形向x轴负方向平移了1个单位 |
| D、关于原点对称 |
 在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点(-3,0)和(1,0).
在平面直角坐标系xOy中,抛物线y=-x2+bx+c经过点(-3,0)和(1,0).