题目内容
二次函数y=
(x-2)2+k,交y轴于点A,B是顶点,P为x轴上一动点,若k=1时△ABP能否成为直角三角形?求P点坐标.
| 1 |
| 4 |
考点:二次函数的性质
专题:
分析:先将k=1代入y=
(x-2)2+k,得y=
(x-2)2+1,则A(0,2),B(2,1),再设P点坐标为(x,0),分三种情况进行讨论:①∠A为直角;②∠B为直角;③∠P为直角.每一种情况都可以根据勾股定理列出关于x的方程,解方程即可求出P点坐标.
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:将k=1代入y=
(x-2)2+k,
得y=
(x-2)2+1,
则A(0,2),B(2,1),
所以AB2=(2-0)2+(1-2)2=5.
设P点坐标为(x,0),分三种情况:
①如果∠A为直角,那么AB2+AP2=BP2,
即5+(x-0)2+(0-2)2=(x-2)2+(0-1)2,
解得x=-1,
所以P点坐标为(-1,0);
②如果∠B为直角,那么AB2+BP2=AP2,
即5+(x-2)2+(0-1)2=(x-0)2+(0-2)2,
解得x=
,
所以P点坐标为(
,0);
③如果∠P为直角,那么AP2+BP2=AB2,
即(x-0)2+(0-2)2+(x-2)2+(0-1)2=5,
整理,得x2-2x+2=0,
∵△=4-4×1×2=-4<0,
∴原方程无解.
综上所述,k=1时△ABP能成为直角三角形,此时P点坐标为(-1,0)或(
,0).
| 1 |
| 4 |
得y=
| 1 |
| 4 |
则A(0,2),B(2,1),
所以AB2=(2-0)2+(1-2)2=5.
设P点坐标为(x,0),分三种情况:
①如果∠A为直角,那么AB2+AP2=BP2,
即5+(x-0)2+(0-2)2=(x-2)2+(0-1)2,
解得x=-1,
所以P点坐标为(-1,0);
②如果∠B为直角,那么AB2+BP2=AP2,
即5+(x-2)2+(0-1)2=(x-0)2+(0-2)2,
解得x=
| 3 |
| 2 |
所以P点坐标为(
| 3 |
| 2 |
③如果∠P为直角,那么AP2+BP2=AB2,
即(x-0)2+(0-2)2+(x-2)2+(0-1)2=5,
整理,得x2-2x+2=0,
∵△=4-4×1×2=-4<0,
∴原方程无解.
综上所述,k=1时△ABP能成为直角三角形,此时P点坐标为(-1,0)或(
| 3 |
| 2 |
点评:本题考查二次函数的性质,二次函数图象上点的坐标特征,勾股定理,注意本题要分三种情况讨论,不要漏解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
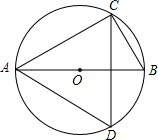 如图,AB是⊙O的直径,点C、D是⊙O上的点,若∠CAB=25°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C、D是⊙O上的点,若∠CAB=25°,则∠ADC的度数为( )| A、65° | B、55° |
| C、60° | D、75° |
 如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线.
如图所示,BE与CD相交于点A,CF为∠BCD的平分线,EF为∠BED的平分线. 如图,⊙O是正五边形ABCDE的外接圆,P是⊙O上任意一点,则∠APB=
如图,⊙O是正五边形ABCDE的外接圆,P是⊙O上任意一点,则∠APB=