题目内容
16. 如图,小刚从点A出发,沿着坡度为α的斜坡向上走了650米到达点B,且
如图,小刚从点A出发,沿着坡度为α的斜坡向上走了650米到达点B,且sinα=$\frac{5}{13}$.
(1)则他上升的高度是250 米;
(2)然后又沿着坡度为i=1:3的斜坡向上走了1000米达到点C.问小刚从A点到C点上升的高度CD是多少米(结果保留根号)?
分析 (1)根据题意画出图形,进而利用锐角三角函数关系分别求出BF;
(2)利用坡度的定义求得CE的长,即可得出点C相对于起点A升高的高度.
解答 解:(1)如图所示:过点B作BF⊥AD于点F,过点C作CD⊥AD于点D,
由题意得:AB=650米,BC=1千米,
∴sinα=$\frac{5}{13}$=$\frac{BF}{AB}$=$\frac{BF}{650}$,
∴BF=650×$\frac{5}{13}$=250(米),
∴小明从A点到点B上升的高度是250米;
(2)∵斜坡BC的坡度为:1:3,
∴CE:BE=1:3,
设CE=x,则BE=3x,
由勾股定理得:x2+(3x)2=10002,
解得:x=100$\sqrt{10}$,
∴CD=CE+DE=BF+CE=250+100$\sqrt{10}$,
答:点C相对于起点A升高了(250+100$\sqrt{10}$)米.
故答案为:250.
点评 此题主要考查了解直角三角形的应用,根据题意构造直角三角形,正确选择锐角三角函数得出BF,CE的长是解题关键.

练习册系列答案
相关题目
7.下表是小明填写实习报告的部分内容:已知:sin47°=0.7313,cos47°=0.6820,tan47°=1.0724,$\frac{1}{{tan{{47}°}}}$=0.9325,根据以上的条件,计算出铁塔顶端到山底的高度( )
| 题目 | 在山脚下测量铁塔顶端到山底的高度 | |
| 测量 目标 图示 |  | 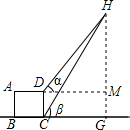 |
| CD=5m | ∠α=45°,∠β=47° | |
| A. | 64.87m | B. | 74.07m | C. | 84.08m | D. | 88.78m |
11. 如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )
如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )
 如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )
如图棋盘上有黑、白两色棋子若干,找出所有三颗颜色相同的棋并且在同一直线上的直线,这样直线共有多少条( )| A. | 6条 | B. | 5条 | C. | 4条 | D. | 3条 |
1.下列结论:
①若关于x的方程ax+b=0(a≠0)的解是x=1,则a+b=0;
②若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=-$\frac{1}{2}$;
③若a+b=1,且a≠0,则x=1一定是方程ax+b=1的解.
其中正确的结论是( )
①若关于x的方程ax+b=0(a≠0)的解是x=1,则a+b=0;
②若b=2a,则关于x的方程ax+b=0(a≠0)的解为x=-$\frac{1}{2}$;
③若a+b=1,且a≠0,则x=1一定是方程ax+b=1的解.
其中正确的结论是( )
| A. | ①② | B. | ②③ | C. | ①③ | D. | ①②③ |
5.如果9a2-ka+4是完全平方式,那么k的值是( )
| A. | -12 | B. | 6 | C. | ±12 | D. | ±6 |