题目内容
20. 如图:四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F.
如图:四边形ABCD是平行四边形,AE⊥BC于E,AF⊥CD于F.(1)若AE=4cm,AF=6cm,AD=9cm,求CD的长;
(2)若?ABCD的周长为40cm,AE=6cm,AF=9cm,求?ABCD的面积.
分析 (1)根据平行三边的面积公式=底×高即可求出CD的长;
(2)根据平行四边形的周长求出BC+CD=20,再根据平行四边形的面积求出BC=CD,然后求出CD的值,再根据平行四边形的面积公式计算即可得解
解答 解:
(1)∵四边形ABCD是平行四边形,
∴AD=BC,
∵AE⊥BC于E,AF⊥CD于F,
∴BC•AE=CD•AF,
∵AE=4cm,AF=6cm,AD=9cm,
∴9×4=CD×6
∴CD=6cm;
(2)∵?ABCD的周长=2(BC+CD)=40,
∴BC+CD=20①,
∵AE⊥BC于E,AF⊥CD于F,AE=6cm,AF=9cm,
∴S?ABCD=6BC=9CD,
整理得,BC=1.5CD②,
联立①②解得,CD=8,
∴?ABCD的面积=AF•CD=6CD=6×8=48.
点评 本题考查了平行四边形的性质,根据平行四边形的周长与面积得到关于BC、CD的两个方程并求出CD的值是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
3.方程x+y=6的正负整数解有( )
| A. | 6组 | B. | 7组 | C. | 8组 | D. | 无数组 |
5.下列函数:①y=2x2+x+1 ②y=3x+1 ③y=x(x-2)-x2 ④y=-x中,是一次函数的有( )个.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
12. 如图,将直角坐标系中“鱼”的图案关于x轴翻折,那么点A的对应点A′的坐标是( )
如图,将直角坐标系中“鱼”的图案关于x轴翻折,那么点A的对应点A′的坐标是( )
 如图,将直角坐标系中“鱼”的图案关于x轴翻折,那么点A的对应点A′的坐标是( )
如图,将直角坐标系中“鱼”的图案关于x轴翻折,那么点A的对应点A′的坐标是( )| A. | (-5,4) | B. | (4,-2) | C. | (5,-2) | D. | (5,-4). |
10.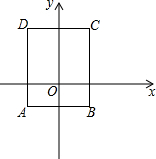 如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),则点C的坐标是( )
如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),则点C的坐标是( )
 如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),则点C的坐标是( )
如图,四边形ABCD是长方形,AB=3,AD=4.已知A(-$\frac{3}{2}$,-1),则点C的坐标是( )| A. | (-3,$\frac{3}{2}$) | B. | ($\frac{3}{2}$,-3) | C. | (3,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,3) |
 如图,如果将△ABC的顶点A向左平移3个单位后再向下平移一个单位到达A′点,连接A′C,那么线段A′C与线段AB的位置关系是( )
如图,如果将△ABC的顶点A向左平移3个单位后再向下平移一个单位到达A′点,连接A′C,那么线段A′C与线段AB的位置关系是( ) 如图,已知直线AB∥CD,∠1=50°,则∠2=50°.
如图,已知直线AB∥CD,∠1=50°,则∠2=50°.