题目内容
如图，在△ABC中，AB、BC的垂直平分线EF、GH相交于点P，且点P在AC上，求证：△ABC是直角三角形．考点：线段垂直平分线的性质
专题：证明题
分析：首先连接PB，由在△ABC中，AB、BC的垂直平分线EF、GH相交于点P，可得PA=PB=PC，继而证得：△ABC是直角三角形．
解答：
证明：连接PB，
∵在△ABC中，AB、BC的垂直平分线EF、GH相交于点P，
∴PA=PB，PB=PC，
∴∠A=∠ABP，∠C=∠CBP，
∵∠A+∠ABP+∠CBP+∠C=180°，
∴∠ABC=∠ABP+∠CBP=90°，
即△ABC是直角三角形．
证明：连接PB，∵在△ABC中，AB、BC的垂直平分线EF、GH相交于点P，
∴PA=PB，PB=PC，
∴∠A=∠ABP，∠C=∠CBP，
∵∠A+∠ABP+∠CBP+∠C=180°，
∴∠ABC=∠ABP+∠CBP=90°，
即△ABC是直角三角形．
点评：此题考查了线段垂直平分线的性质以及直角三角形的性质．此题难度不大，注意掌握数形结合思想的应用．
练习册系列答案
新思维寒假作业系列答案
相关题目
如图，若∠ABC+∠CDE-∠C=180°，试证明：AB∥DE．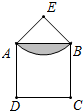
如图所示，△EBA是等边三角形，□ABCD边长为6，E是过A、B两点圆弧的圆心，求阴影部分面积．