题目内容
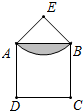 如图所示,△EBA是等边三角形,□ABCD边长为6,E是过A、B两点圆弧的圆心,求阴影部分面积.
如图所示,△EBA是等边三角形,□ABCD边长为6,E是过A、B两点圆弧的圆心,求阴影部分面积.考点:扇形面积的计算
专题:
分析:利用正三角形的性质以及正方形的性质得出AE,BE的长,再利用勾股定理求出EF的长,进而利用扇形面积公式以及三角形面积求法得出即可.
解答: 解:过点E作EF⊥AB于点F,
解:过点E作EF⊥AB于点F,
∵△EBA是等边三角形,□ABCD边长为6,
∴AE=BE=AB=6,
∴AF=BF=3,
∴EF=
=3
,
∴S△AEB=
×EF×AB=
×6×3
=9
,
S扇形EAB=
π×62=6π,
∴阴影部分面积为:6π-9
.
 解:过点E作EF⊥AB于点F,
解:过点E作EF⊥AB于点F,∵△EBA是等边三角形,□ABCD边长为6,
∴AE=BE=AB=6,
∴AF=BF=3,
∴EF=
| 62-32 |
| 3 |
∴S△AEB=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 3 |
S扇形EAB=
| 60 |
| 360 |
∴阴影部分面积为:6π-9
| 3 |
点评:此题主要考查了扇形面积求法以及等边三角形的性质,得出EF的长是解题关键.

练习册系列答案
相关题目
 如图,在△ABC中,AB、BC的垂直平分线EF、GH相交于点P,且点P在AC上,求证:△ABC是直角三角形.
如图,在△ABC中,AB、BC的垂直平分线EF、GH相交于点P,且点P在AC上,求证:△ABC是直角三角形. 如图,AB=AC,AD=AE,求证:DE⊥BC.
如图,AB=AC,AD=AE,求证:DE⊥BC.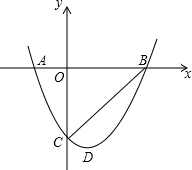 如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.
如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.