题目内容
观察下面的一列数,按照它们排列规律再写出接下的三个数,描述这列数的规律,并写出第2011数.
+
,-
,+
,-
,+
, , , .
+
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
考点:规律型:数字的变化类
专题:
分析:分子是连续的奇数,分母是连续的偶数,奇数位置为正,偶数位置为负,第n个数为(-1)n+1
,由此规律得出答案即可.
| 2n-1 |
| 2n |
解答:解:数列为:+
,-
,+
,-
,+
,-
,+
,-
,…;
第2011个数为+
.
故答案为:-
,+
,-
.
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
第2011个数为+
| 4021 |
| 4022 |
故答案为:-
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
点评:此题考查数字的变化规律,找出数字之间的联系,得出规律,利用规律解决问题.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,在△ABC中,AB、BC的垂直平分线EF、GH相交于点P,且点P在AC上,求证:△ABC是直角三角形.
如图,在△ABC中,AB、BC的垂直平分线EF、GH相交于点P,且点P在AC上,求证:△ABC是直角三角形. 如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.
如图所示图形,用代数式表示该图形的面积,并计算当x=10,y=14时,图形的面积.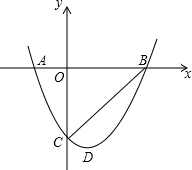 如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.
如图,已知抛物线y=x2-2x-3与x轴从左至右分别交于A、B两点,与y轴交于C点,顶点为D.