题目内容
一个多边形的边长分别为2，3，4，5，6，另一个和它相似的多边形的最短边长为6，求较大多边形的周长．
考点：相似多边形的性质
专题：
分析：设较大多边形的周长为x，求出多边形的周长，再根据相似多边形的周长的比等于相似比列式计算即可得解．
解答：解：设较大多边形的周长为x，
多边形的周长=2+3+4+5+6=20，
∵两多边形相似，
∴
=
，
解得x=60．
答：较大多边形的周长是60．
多边形的周长=2+3+4+5+6=20，
∵两多边形相似，
∴
| x |
| 20 |
| 6 |
| 2 |
解得x=60．
答：较大多边形的周长是60．
点评：本题考查了相似多边形的性质，熟记相似多边形的周长的比等于相似比是解题的关键．
练习册系列答案
相关题目
下列各式中用科学记数法表示正确的是（ ）
| A、0.05=5×10-3 |
| B、0.0034=34×10-3 |
| C、-0.00012=1.2×10-4 |
| D、2.12=2.12×100 |
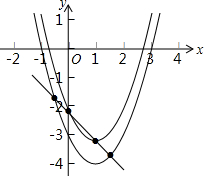如图，抛物线c1：y=（x-1）2-
平行四边形ABCD中，AE⊥BC于E，AF⊥CD于F，∠EAF=60°，若CF=2，CE=3，求平行四边形ABCD周长．
如图，在△ABC中，AB、BC的垂直平分线EF、GH相交于点P，且点P在AC上，求证：△ABC是直角三角形．
如图，AB=AC，AD=AE，求证：DE⊥BC．