题目内容
如图，在矩形ABCD中，E、F分别是DC、BC边上的点，且∠AEF=90°则下列结论正确的是（ ）
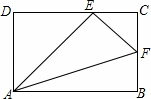
A． △ABF∽△AEF B． △ABF∽△CEF C． △CEF∽△DAE D． △DAE∽△BAF
C
考点： 相似三角形的判定．
分析： 利用等角的余角相等可得∠DAE=∠CEF，加上∠D=∠C=90°，则根据有两组角对应相等的两个三角形相似可判断△CEF∽△DAE．
解答： 解：∵∠AEF=90°，
∴∠ADE+∠CEF=90°，
而∠ADE+∠DAE=90°，
∴∠DAE=∠CEF，
而∠D=∠C=90°，
∴△CEF∽△DAE．
故选C．
点评： 本题考查了相似三角形的判定：有两组角对应相等的两个三角形相似．也考查了矩形的性质．
练习册系列答案
相关题目
=
×
C． （3a2）3=9a6 D． 
+
=3