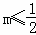题目内容
如图,D是AC上一点,BE∥AC,BE=AD,AE分别交BD、BC于点F、G,∠1=∠2.
求证:FD2=FG•FE.
考点: 相似三角形的判定与性质;平行四边形的判定.
专题: 证明题.
分析: 根据BE∥AC,BE=AD,可得ABED为平行四边形,FD=FB.欲证FD2=FG•FE,则证FB2=FG•FE,即证FB:FG=FE:FB.易证它们所在的三角形相似.
解答: 证明:∵BE∥AC,
∴∠1=∠E. (2分)
∵∠1=∠2,
∴∠2=∠E. (4分)
又∵∠BFG=∠EFB,
∴△BFG∽△EFB. (5分)
∴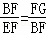 ,
,
∴BF2=FG•EF. (6分)
∵BE∥AC,BE=AD,
∴ABED为平行四边形,FD=FB.
∴FD2=FG•FE. (10分)
点评: 此题考查了相似三角形的判定和性质,利用平行四边形的性质进行线段转换,有一定难度.证线段的乘积相等,通常转化为比例式形式,再证明所在的三角形相似.

练习册系列答案
相关题目