Question

【题目】如图，在Rt△ABC中，∠ACB=90°，AB=10，BC=6，点O在射线上（点不与点重合），过点作，垂足为，以点为圆心，为半径画半圆，分别交射线于、两点，设．

（1）如图，当点为边的中点时，求的值；

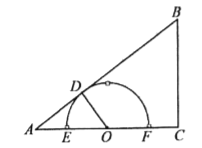
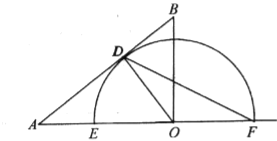
（2）如图，当点与点重合时，连接，求弦的长；

（3）当半圆与无交点时，直接写出的取值范围．

Answer 1

【答案】（1）；（2）；（3）0＜x＜3或x＞12

【解析】

（1）首先由勾股定理求出AC的长，再证明△AOD∽△ABC，得，代入相关数据从而可求出OD；

（2）首先根据等积法求出OD，再过点D作DH⊥AC，证明△DOH∽△ABO，求出DH、OH，最后在直角三角形DFH中运用勾股定理求出DF的长即可；

（3）分点O在点C左侧和点C右侧两种情况，运用相似三角形的性质求解即可．

（1）在Rt△ABC中，∵AB=10，BC=6，

∴，

∵点O为AC边的中点，

∴．

∵OD⊥AB，∠ACB=90°，

∴∠ADO=∠ACB，

又∵∠A=∠A，

∴△AOD∽△ABC．

∴，即，∴．

（2） ∵点O与点C重合，OD⊥AB,

∴OD·AB=AC·BC，即10x=8×6，

∴． 即OD=

过点D作DH⊥AC，垂足为H，则有∠DHO=∠ACB=90°．

∵∠DOH+∠BOD=90°，∠ABO+∠BOD=90°，

∴∠DOH=∠ABO，

∴△DOH∽△ABO，

∴，即，

∴，．

∵OF=OD=，

∴FH=OH+OF=．

∴在Rt△DFH中，根据勾股定理，得：

∴．

（3）①当点O在点C左侧，且与BC相切时，如图，

设OD=x，则OC=x，

∴AO=8-x，

∵∠ADO=∠ACB，∠A=∠A，

∴△AOD∽△ABC，

∴，

∵AB=10，BC=6，AO=8-x，

∴，解得，x=3,

∴当半圆O在BC的左侧，且与BC无交点时，x的取值范围为：0＜x＜3；

②当点O在点C右侧，且与BC相切时，如图，

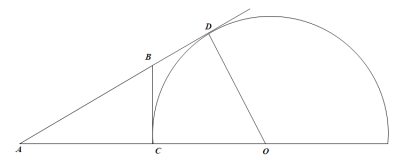
方法同①，得x=12，

∴当半圆O在BC的右侧，且与BC无交点时，x的取值范围为： x＞12；

综上，当半圆与无交点时，x的取值范围是0＜x＜3或x＞12．