��Ŀ����
19��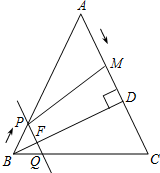 ��ͼ���ڡ�ABC�У�AB=AC=10cm��BD��AC�ڵ�D����BD=8cm����M�ӵ�A��������AC�ķ��������˶����ٶ�Ϊ2cm/�룻ͬʱֱ��PQ�ɵ�B��������BA�ķ��������˶����ٶ�Ϊ1cm/�룬�˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB�ڵ�P����BC�ڵ�Q����BD�ڵ�F������PM�����˶�ʱ��Ϊt�루0��t��5����
��ͼ���ڡ�ABC�У�AB=AC=10cm��BD��AC�ڵ�D����BD=8cm����M�ӵ�A��������AC�ķ��������˶����ٶ�Ϊ2cm/�룻ͬʱֱ��PQ�ɵ�B��������BA�ķ��������˶����ٶ�Ϊ1cm/�룬�˶�������ʼ�ձ���PQ��AC��ֱ��PQ��AB�ڵ�P����BC�ڵ�Q����BD�ڵ�F������PM�����˶�ʱ��Ϊt�루0��t��5������1����tΪ��ֵʱ���ı���PQCM��ƽ���ı��Σ�
��2�����ı���PQCM�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ��
���� ��1������PQCMΪƽ���ı��Σ�����ƽ���ı��ε����ʵõ��Ա�ƽ�У������õ�AP=AM���г�����t�ķ��̣�������̵Ľ�õ���������t��ֵ��
��2������PQ��AC�ɵá�PBQ�ס�ABC���������������ε���״��Ȼ��ͬ��֪������BPQҲΪ���������Σ���BP=PQ=t������֤�õ����������εõױȵ��ڸ߱ȸߣ��ú�t�Ĵ���ʽ�Ϳ��Ա�ʾ��BF�������õ����εĸ�PE=DF=8-t���ֵ�M���˶��ٶȺ�ʱ���֪��M�߹���·��AM=2t���������ε��µ�CM=10-2t�����������ε������ʽ���ɵõ�y��t�Ĺ�ϵʽ��
���  �⣺��1�������ı���PQCM��ƽ���ı��Σ���PM��QC��
�⣺��1�������ı���PQCM��ƽ���ı��Σ���PM��QC��
��AP��AB=AM��AC��
��AB=AC��
��AP=AM����10-t=2t��
���t=$\frac{10}{3}$��
�൱t=$\frac{10}{3}$sʱ���ı���PQCM��ƽ���ı��Σ�
��2����PQ��AC��
���PBQ�ס�ABC��
���PBQ����������PQ=PB=t��
��$\frac{BF}{BD}$=$\frac{BP}{BA}$����$\frac{BF}{8}$=$\frac{t}{10}$��
���BF=$\frac{4}{5}$t��
��FD=BD-BF=8-$\frac{4}{5}$t��
�֡�MC=AC-AM=10-2t��
��y=$\frac{1}{2}$��PQ+MC��•FD=$\frac{1}{2}$��t+10-2t����8-$\frac{4}{5}$t��=$\frac{2}{5}$t2-8t+40��
���� �����ۺϿ�����ƽ���ı��ε����ʣ����������Ƶ��ж������ʣ��ڶ��ʵĽ���ؼ��Ǹ������������εĸ�֮�ȵ��ڶ�Ӧ��֮�ȵó����������������ϵʽ��

 ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�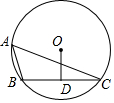 ��ͼ����O�İ뾶��Ϊ2����A��B��C�ڡ�O�ϣ���BAC=60�㣬OD��BC��D����OD�ij��ǣ�������
��ͼ����O�İ뾶��Ϊ2����A��B��C�ڡ�O�ϣ���BAC=60�㣬OD��BC��D����OD�ij��ǣ�������| A�� | 1 | B�� | 1.5 | C�� | $\sqrt{2}$ | D�� | $\sqrt{3}$ |
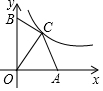 ��ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���x�ᡢy����������ϣ�OA=6��OB=9����C�ں���y=$\frac{k}{x}$��x��0����ͼ���ϣ�����C�ĺ�����Ϊ4ʱ����OAC���OBC�������ȣ�k��ֵΪ��������
��ͼ����ƽ��ֱ������ϵ�У���A��B�ֱ���x�ᡢy����������ϣ�OA=6��OB=9����C�ں���y=$\frac{k}{x}$��x��0����ͼ���ϣ�����C�ĺ�����Ϊ4ʱ����OAC���OBC�������ȣ�k��ֵΪ��������| A�� | 16 | B�� | 24 | C�� | 30 | D�� | 36 |
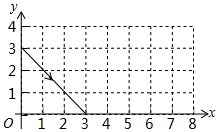 ��ͼ������P�ӣ�0��3������������ʾ�����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����P��17���������εı�ʱ����P������Ϊ��������
��ͼ������P�ӣ�0��3������������ʾ�����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����P��17���������εı�ʱ����P������Ϊ��������| A�� | ��3��0�� | B�� | ��0��3�� | C�� | ��1��4�� | D�� | ��8��3�� |
| A�� | $\frac{1}{28}$ | B�� | $\frac{1}{29}$ | C�� | $\frac{1}{30}$ | D�� | $\frac{1}{31}$ |
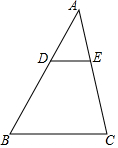 ��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬��DE��BC��AD=2��DB=3����ADE������2�����ı���BCED������ǣ�������
��ͼ��D��E�ֱ��ǡ�ABC�ı�AB��AC�ϵĵ㣬��DE��BC��AD=2��DB=3����ADE������2�����ı���BCED������ǣ�������| A�� | 4 | B�� | 8 | C�� | $\frac{21}{2}$ | D�� | $\frac{25}{2}$ |
| A�� | 63.2��104 | B�� | 6.32��105 | C�� | 0.632��106 | D�� | 6.32��106 |