题目内容
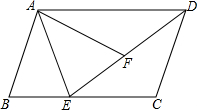 如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的角平分线.求证:
如图,在平行四边形ABCD中,∠B=∠AFE,EA是∠BEF的角平分线.求证:(1)△ABE≌△AFE;
(2)∠FAD=∠CDE.
考点:平行四边形的性质,全等三角形的判定与性质
专题:证明题
分析:(1)根据角平分线的性质可得∠1=∠2,再加上条件∠B=∠AFE,公共边AE,可利用AAS证明△ABE≌△AFE;
(2)首先证明AF=CD,再证明∠B=∠AFE,∠AFD=∠C可证明△AFD≌△DCE进而得到∠FAD=∠CDE.
(2)首先证明AF=CD,再证明∠B=∠AFE,∠AFD=∠C可证明△AFD≌△DCE进而得到∠FAD=∠CDE.
解答: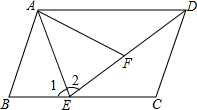 证明:(1)∵EA是∠BEF的角平分线,
证明:(1)∵EA是∠BEF的角平分线,
∴∠1=∠2,
在△ABE和△AFE中,
,
∴△ABE≌△AFE(AAS);
(2)∵△ABE≌△AFE,
∴AB=AF,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥CB,AB∥CD,
∴AF=CD,∠ADF=∠DEC,∠B+∠C=180°,
∵∠B=∠AFE,∠AFE+∠AFD=180°,
∴∠AFD=∠C,
在△AFD和△DCE中,
,
∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
 证明:(1)∵EA是∠BEF的角平分线,
证明:(1)∵EA是∠BEF的角平分线,∴∠1=∠2,
在△ABE和△AFE中,
|
∴△ABE≌△AFE(AAS);
(2)∵△ABE≌△AFE,
∴AB=AF,
∵四边形ABCD是平行四边形,
∴AB=CD,AD∥CB,AB∥CD,
∴AF=CD,∠ADF=∠DEC,∠B+∠C=180°,
∵∠B=∠AFE,∠AFE+∠AFD=180°,
∴∠AFD=∠C,
在△AFD和△DCE中,
|
∴△AFD≌△DCE(AAS),
∴∠FAD=∠CDE.
点评:此题主要考查了平行四边形的性质,以及全等三角形的判定与性质,关键是正确证明△AFD≌△DCE.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
 已知的图象如图所示,当y<0时,x的取值范围是( )
已知的图象如图所示,当y<0时,x的取值范围是( )| A、x>-3 | B、x<-3 |
| C、x>1 | D、x<1 |
 先完成填空,再按要求答题:
先完成填空,再按要求答题: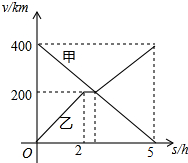 甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题:
甲,乙两辆汽车分别从A,B两地同时出发,沿同一条公路相向而行,乙车出发2h后休息,与甲车相遇后,继续行驶.设甲、乙两车与B地的路程分别为y甲(km),y乙(km),甲车行驶的时间为x(h),y甲,y乙与x之间的函数图象如图所示,结合图象解答下列问题: 如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°.
如图,点B、C、D都在半径为6的⊙O上,过点C作AC∥BD交OB的延长线于点A,连接CD,已知∠CDB=∠OBD=30°. 如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数.
如图,已知∠DAB=70°,AC平分∠DAB,∠1=35°,求∠D的度数. 如图,∠A=15°,AB=BC=CD=DE=EF,则∠GEF=
如图,∠A=15°,AB=BC=CD=DE=EF,则∠GEF=