题目内容
如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.
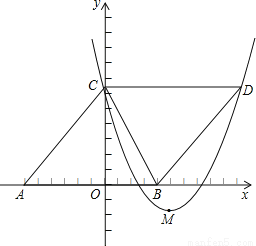
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
【解析】 (1)证明:∵A(﹣6,0),B(4,0),C(0,8), ∴AB=6+4=10,。∴AB=AC。 由翻折可得,AB=BD,AC=CD。∴AB=BD=CD=AC。∴四边形ABCD是菱形。 ∴CD∥AB。 ∵C(0,8),∴点D的坐标是(10,8)。 (2)∵y=ax2﹣10ax+c,∴对称轴为直线。 设M的坐标为(5,n),直线BC的解析式为y=kx...
练习册系列答案
相关题目


 B. 22×23=26 C. 20=0 D. (﹣1)﹣2=1
B. 22×23=26 C. 20=0 D. (﹣1)﹣2=1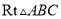 ,
, 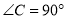 ,若
,若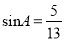 ,
, 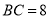 ,则
,则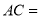 __________.
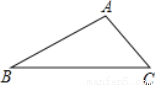
__________.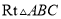 中,
中, 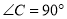 ,
, 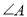 、
、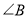 的对边是
的对边是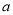 、
、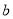 ,且满足
,且满足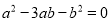 ,则
,则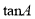 等于( ).
等于( ).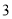 B.
B. 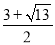 C.
C. 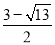 D.
D. 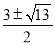
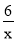 图象上的概率.
图象上的概率.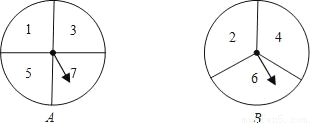
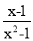 +
+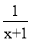 )÷
)÷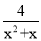 =_____.
=_____.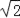 千米.(注:结果有根号的保留根号)
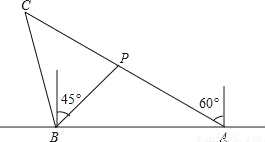
千米.(注:结果有根号的保留根号)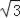 千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.
千米/时的速度进行沿途考察,航行一段时间后到达点C处,此时,从B测得小船在北偏西15°方向,求小船沿途考察的时间.