题目内容
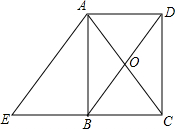如图，已知矩形ABCD中，对角线AC、BD相交于点O，过点A作AE∥BD，交CB的延长线于点E．（1）求证：AE=AC；
（2）若cosE=
| 3 |
| 5 |
考点：矩形的性质
专题：
分析：（1）由矩形的性质，可得AC=BD，欲求AC=AE，证BD=AE即可．可通过证四边形AEBD是平行四边形，从而得出AC=AE的结论；
（2）首先根据等腰三角形的性质得到EB的长，然后利用锐角三角函数求得AE的长，从而利用勾股定理求得AB的长，最后求得面积即可．
（2）首先根据等腰三角形的性质得到EB的长，然后利用锐角三角函数求得AE的长，从而利用勾股定理求得AB的长，最后求得面积即可．
解答：解：（1）证明：在矩形ABCD中，AC=BD，AD∥BC，
又∵AE∥BD，
∴四边形AEBD是平行四边形．
∴BD=AE，
∴AC=AE；
（2）∵AE=AC，AB⊥EC，
∴EB=BC，
∵CE=6，
∴EB=3，
∵cosE=
=
，
∴AE=5，
∴由勾股定理得：AB=4，
∴矩形ABCD的面积为4×3=12．
又∵AE∥BD，
∴四边形AEBD是平行四边形．
∴BD=AE，
∴AC=AE；
（2）∵AE=AC，AB⊥EC，
∴EB=BC，
∵CE=6，
∴EB=3，
∵cosE=
| EB |
| AE |
| 3 |
| 5 |
∴AE=5，
∴由勾股定理得：AB=4，
∴矩形ABCD的面积为4×3=12．
点评：本题考查了矩形的性质，了解矩形的特殊性质是解答本题的关键，本题难度不大，但综合性较强．
练习册系列答案
相关题目
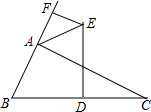已知：△ABC，DE垂直平分BC边，∠BAC外角平分线与DE交于E，过E作EF垂直直线AB于F．若AF=2，AB=3，那么AC长是
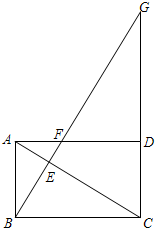已知：矩形ABCD中，过点B作 BG⊥AC交AC于点E，分别交射线AD于F点、交射线CD于G点，BC=6．