题目内容
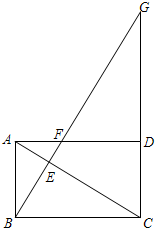 已知:矩形ABCD中,过点B作 BG⊥AC交AC于点E,分别交射线AD于F点、交射线CD于G点,BC=6.
已知:矩形ABCD中,过点B作 BG⊥AC交AC于点E,分别交射线AD于F点、交射线CD于G点,BC=6.(1)当点F为AD中点时,求AB的长;
(2)联结AG,设AB=x,S△AFG=y,求y关于x的函数关系式及自变量x的取值范围;
(3)是否存在x的值,使以D为圆心的圆与BC、BG都相切?若存在,求出x的值;若不存在,请说明理由.
考点:相似形综合题
专题:综合题
分析:(1)易证△ABF∽△BCA,然后根据相似三角形的性质就可求出AB的值;
(2)由(1)可得△ABF∽△BCA,根据相似三角形的性质就可求得AF=
,同理可得CG=
.然后分点F在线段AD上及在线段AD延长线上两种情况进行讨论,只需求出AF、DG,就可解决问题;
(3)过点D作DH⊥BG于点H,易得∠ACB=30°,在Rt△ABC中运用三角函数就可解决问题.
(2)由(1)可得△ABF∽△BCA,根据相似三角形的性质就可求得AF=
| x2 |
| 6 |
| 36 |
| x |
(3)过点D作DH⊥BG于点H,易得∠ACB=30°,在Rt△ABC中运用三角函数就可解决问题.
解答:解:(1)∵点F为AD中点,且AD=BC=6,
∴AF=3.
∵矩形ABCD中,∠ABC=90°,BG⊥AC于点E,
∴∠ABE+∠EBC=90°,∠ACB+∠EBC=90°,
∴∠ABE=∠ACB.
∵∠FAB=∠ABC=90°,
∴△ABF∽△BCA,
∴
=
,
∴
=
,
∴AB=3
;
(2)由(1)可得△ABF∽△BCA,
∴
=
.
∵AB=x,BC=6,
∴AF=
=
,
同理可得:CG=
=
.
①当F点在线段AD上时,如图1,

DG=CG-CD=
-x=
,
∴S△AFG=
AF•DG=
,
即y=
(0<x<6);
②当F点在线段AD延长线上时,如图2,

DG=CD-CG=x-
=
,
∴S△AFG=
AF•DG=
,
即y=
(x>6);
(3)过点D作DH⊥BG于点H,如图3,

∵以点D为圆心的圆与BC、BG都相切,
∴CD=DH,
∴∠DBF=∠CBD.
∵矩形ABCD中,∠ACB=∠CBD,
∴Rt△BEC中,∠ACB+∠CBD+∠DBF=90°,
∴∠ACB=30°,
∴Rt△ABC中,tan∠ACB=
,
∴tan30°=
,
∴x=2
,
即当x=2
时,以点D为圆心的圆与BC、BG都相切.
∴AF=3.
∵矩形ABCD中,∠ABC=90°,BG⊥AC于点E,
∴∠ABE+∠EBC=90°,∠ACB+∠EBC=90°,
∴∠ABE=∠ACB.
∵∠FAB=∠ABC=90°,
∴△ABF∽△BCA,
∴
| AB |
| BC |
| AF |
| BA |
∴
| AB |
| 6 |
| 3 |
| AB |
∴AB=3
| 2 |
(2)由(1)可得△ABF∽△BCA,
∴
| AB |
| BC |
| AF |
| AB |
∵AB=x,BC=6,
∴AF=
| AB2 |
| BC |
| x2 |
| 6 |
同理可得:CG=
| BC2 |
| AB |
| 36 |
| x |
①当F点在线段AD上时,如图1,

DG=CG-CD=
| 36 |
| x |
| 36-x2 |
| x |
∴S△AFG=
| 1 |
| 2 |
| 36x-x3 |
| 12 |
即y=
| 36x-x3 |
| 12 |
②当F点在线段AD延长线上时,如图2,

DG=CD-CG=x-
| 36 |
| x |
| x2-36 |
| x |
∴S△AFG=
| 1 |
| 2 |
| x3-36x |
| 12 |
即y=
| x3-36x |
| 12 |
(3)过点D作DH⊥BG于点H,如图3,

∵以点D为圆心的圆与BC、BG都相切,
∴CD=DH,
∴∠DBF=∠CBD.
∵矩形ABCD中,∠ACB=∠CBD,
∴Rt△BEC中,∠ACB+∠CBD+∠DBF=90°,
∴∠ACB=30°,
∴Rt△ABC中,tan∠ACB=
| AB |
| BC |
∴tan30°=
| x |
| 6 |
∴x=2
| 3 |
即当x=2
| 3 |
点评:本题主要考查了相似三角形的判定与性质、矩形的性质、切线长定理、三角函数等知识,运用分类讨论的思想是解决第(2)小题的关键.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
已知平行四边形ABCD,下列判断正确的是( )
| A、若∠A=90°,则四边形ABCD是矩形 |
| B、AC=BD |
| C、AB=CD,则ABCD是菱形 |
| D、若AC丄BD,则四边形ABCD为正方形 |
平面直角坐标系内一点P(-6,5)关于原点对称点的坐标是( )
| A、(6,-5) |
| B、(-6,-5) |
| C、(5,-6) |
| D、(6,5) |
计算
+
-
的结果是( )
| 2x |
| x-y |
| x-2y |
| y-x |
| y |
| x-y |
| A、1 | ||
| B、3 | ||
C、
| ||
D、
|
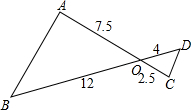 如图,AC,BD相交于点O,问图中的△AOB和△COD是否相似?若相似,请给出证明;若不相似,请说明理由.
如图,AC,BD相交于点O,问图中的△AOB和△COD是否相似?若相似,请给出证明;若不相似,请说明理由.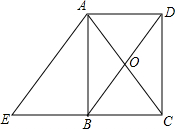 如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AE∥BD,交CB的延长线于点E.
如图,已知矩形ABCD中,对角线AC、BD相交于点O,过点A作AE∥BD,交CB的延长线于点E.