题目内容

18．甲、乙、丙三种扑克牌背面分别相同，三张甲牌正面标有数字1，2，3；三张乙牌正面标有数字2，3，5；二张丙牌正面标有数字3，4．现将它们背面朝上，洗匀后从中分别各抽一张，以正面上的数字作为线段长度．则能构成等腰三角形的概率为$\frac{7}{18}$．

分析 先画树状图展示所有18种等可能的结果数，再根据等腰三角形的判定定理找出其中能构成等腰三角形的结果数，然后根据概率公式求解．

解答 解：画树状图为：

共有18种等可能的结果数，其中能构成等腰三角形的结果数为7（1、3、3，2、2、3，2、3、3，3、2、3，3、3、3，3、3、4，3、5、3），
所以能构成等腰三角形的概率=$\frac{7}{18}$．
故答案为$\frac{7}{18}$．

点评 本题考查了列表法与树状图法：利用列表法和树状图法展示所有可能的结果求出n，再从中选出符合事件A或B的结果数目m，求出概率．也考查了等腰三角形的判定．

练习册系列答案
相关题目
11．观察下列一列数：1，-2，-3，4，-5，-6，7，-8，-9，…
（1）请写出这一列数中第100个数和第2013个数
（2）在前2013个数中，正数和负数分别有多少个？
（3）2015和-2015是否在这一列数中，若在，请写出它们分别是第几个数？若不在，请说明理由．
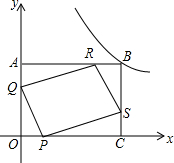9．如图，反比例函数y=$\frac{24}{x}$（x＞0）的图象经过矩形OABC的顶点B（m+2，m），点P从原点O出发沿线段OC向点C运动，点R从点B出发沿线段BA向点A运动，点P、R速度均为每秒1个单位，点Q从O出发沿折线OA→AB向点B运动，点S从点B出发沿折线BC→CO向点O运动，点Q、S速度均为每秒2个单位，设P、Q、R、S四点同时出发，运动时间为t秒（0＜t≤5）
（1）求出OA、OC的长；
（2）当0＜t＜2时，求证：四边形PQRS是平行四边形；
（3）当t为何值时，四边形PQRS是菱形，当t为何值时，四边形PQRS是矩形．
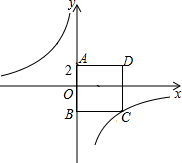6．如图，四边形ABCD为正方形，点A的坐标为（0，2），点B的坐标为（0，-3），反比例函数y1=$\frac{k}{x}$的图象经过点C，一次函数y2=ax+b的图象经过点A、C．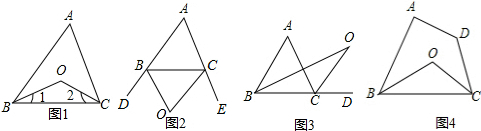
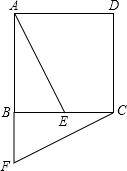（1）求反比例函数和一次函数的表达式；
（2）直接写出y2＞y1时x的取值范围；
（3）若点P是反比例函数图象上的一点，△OAP的面积恰好等于正方形ABCD的面积，求点P的坐标．
13．认真阅读下面关于三角形内外角平分线所夹角的探究片段，完成所提出的问题．
探究1：如图1，在△ABC中，O是∠ABC与∠ACB的平分线BO和CO的交点．通过分析发现$∠BOC={90°}+\frac{1}{2}∠A$．理由如下：
∵BO和CO分别是∠ABC和∠ACB的平分线
∴$∠1=\frac{1}{2}∠ABC，∠2=\frac{1}{2}∠ACB$．
∴∠1+∠2=$\frac{1}{2}$（∠ABC+∠ACB）．
∵∠ABC+∠ACB=180°-∠A，
∴$∠1+∠2=\frac{1}{2}（{180°}-∠A）={90°}-\frac{1}{2}∠A$，
∴$∠BOC={180°}-（∠1+∠2）={180°}-（{90°}-\frac{1}{2}∠A）={90°}+\frac{1}{2}∠A$．
（1）探究2：如图2，O是外角∠DBC与外角∠ECB的平分线BO和CO的交点，则∠BOC与∠A有怎样的关系？请说明理由．
（2）探究3：如图3中，O是∠ABC与外角∠ACD的平分线BO和CO的交点，试分析∠BOC与∠A有怎样的关系？∠BOC=90°-$\frac{1}{2}$∠A （直接写出结论）
（3）拓展：如图4，在四边形ABCD中，O是∠ABC与∠DCB的平分线BO和CO的交点，则∠BOC与∠A+∠D有怎样的关系？∠BOC=$\frac{1}{2}$（∠A+∠D）（直接写出结论）
3．如图所示，正方形ABCD中E为BC的中点，将面ABE旋转后得到△CBF．
（1）指出旋转中心及旋转角度．
（2）判断AE与CF的位置关系．
（3）如果正方形的面积为18cm2，△BCF的面积为4cm2．问四边形AECD的面积是多少？
10．-8x6=-2x23
a6b9c12=a2b3c43
（$\frac{1}{3}$）0$÷（-\frac{1}{3}）$-2=$\frac{1}{9}$．
7．“⊕”表示一种运算符号，其意义是a⊕b=2a-b，若x⊕（1⊕3）=2，则x等于（　　）
A．$\frac{3}{2}$B．2C．$\frac{1}{2}$D．1
8．函数y=$\frac{x+3}{1-x}$的自变量x的取值范围是≠1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网