题目内容
3.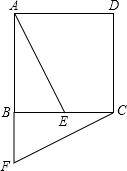 如图所示,正方形ABCD中E为BC的中点,将面ABE旋转后得到△CBF.
如图所示,正方形ABCD中E为BC的中点,将面ABE旋转后得到△CBF.(1)指出旋转中心及旋转角度.
(2)判断AE与CF的位置关系.
(3)如果正方形的面积为18cm2,△BCF的面积为4cm2.问四边形AECD的面积是多少?
分析 (1)先根据正方形的性质得到BA=BC,∠ABC=90°,由于△ABE旋转后得到△CBF,则BC与BA为对应相等,所以根据旋转的定义可判断旋转中心为点B,旋转角度为90°;
(2)由△ABE绕点B顺时针旋转90°得到△CBF可得AE也旋转了90°得到CF,所以AE与CF垂直;
(3)根据旋转的性质得△ABE≌△CBF,则S△CBF=S△ABE=4cm2,然后利用四边形AECD的面积=S正方形ABCD-S△CBF进行计算即可.
解答 解:(1)∵四边形ABCD为正方形,
∴BA=BC,∠ABC=90°,
∵△ABE旋转后得到△CBF,
∴旋转中心为点B,旋转角度为90°;
(2)∵△ABE绕点B顺时针旋转90°得到△CBF,
∴AE⊥CF;
(3)∵△ABE绕点B顺时针旋转90°得到△CBF,
∴△ABE≌△CBF,
∴S△CBF=S△ABE=4cm2,
∴四边形AECD的面积=S正方形ABCD-S△CBF=18-4=10(cm2).
点评 本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了正方形的性质.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
8.某元素原子的直径为0.0006纳米(1纳米=10-9米),相当于( )
| A. | 6×10-4米 | B. | 6×10-10米 | C. | 6×10-13米 | D. | 6×10-12米 |
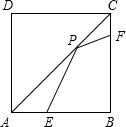 如图,正方形ABCD的边长为8,AE=3,CF=1,点P是对角线AC上一动点,则PE+PF的最小值4$\sqrt{5}$.
如图,正方形ABCD的边长为8,AE=3,CF=1,点P是对角线AC上一动点,则PE+PF的最小值4$\sqrt{5}$.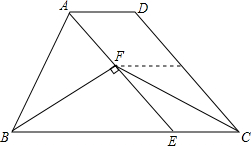 如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.
如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.