题目内容
6.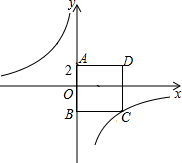 如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y1=$\frac{k}{x}$的图象经过点C,一次函数y2=ax+b的图象经过点A、C.
如图,四边形ABCD为正方形,点A的坐标为(0,2),点B的坐标为(0,-3),反比例函数y1=$\frac{k}{x}$的图象经过点C,一次函数y2=ax+b的图象经过点A、C.(1)求反比例函数和一次函数的表达式;
(2)直接写出y2>y1时x的取值范围;
(3)若点P是反比例函数图象上的一点,△OAP的面积恰好等于正方形ABCD的面积,求点P的坐标.
分析 (1)先根据正方形的性质求出点C的坐标为(5,-3),再将C点坐标代入反比例函数y1=$\frac{k}{x}$中,运用待定系数法求出反比例函数的解析式;同理,将点A,C的坐标代入y=ax+b中,运用待定系数法求出一次函数函数的解析式;
(2)求得反比例函数和一次函数的交点坐标,根据图象即可求得;
(3)设P点的坐标为(x,y),先由△OAP的面积恰好等于正方形ABCD的面积,列出关于x的方程,解方程求出x的值,再将x的值代入y=-$\frac{15}{x}$,即可求出P点的坐标.
解答 解:(1)∵点A的坐标为(0,2),点B的坐标为(0,-3),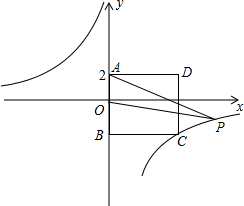
∴AB=5,
∵四边形ABCD为正方形,
∴点C的坐标为(5,-3)
∵反比例函数y1=$\frac{k}{x}$的图象经过点C,
∴-3=$\frac{k}{5}$,解得k=-15,
∴反比例函数的解析式为y1=-$\frac{15}{x}$;
∵一次函数y2=ax+b的图象经过点A,C,
∴$\left\{\begin{array}{l}{b=2}\\{5a+b=-3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=-1}\\{b=2}\end{array}\right.$,
∴一次函数的解析式为y2=-x+2;
(2)解$\left\{\begin{array}{l}{y=-\frac{15}{x}}\\{y=-x+2}\end{array}\right.$得$\left\{\begin{array}{l}{x=5}\\{y=-3}\end{array}\right.$或$\left\{\begin{array}{l}{x=-3}\\{y=5}\end{array}\right.$,
∴交点坐标为(5,-3),(-3,5),
由图象知:当x<-3或0<x<5时,y2>y1;
(3)设P点的坐标为(x,y),
∵△OAP的面积恰好等于正方形ABCD的面积,
∴$\frac{1}{2}$×OA•|x|=52,
∴$\frac{1}{2}$×2|x|=25,解得x=±25.
当x=25时,y=-$\frac{15}{25}$=-$\frac{3}{5}$,
当x=-25时.y=$\frac{15}{25}$=$\frac{3}{5}$,
∴P点的坐标为(25,-$\frac{3}{5}$)或(-25,$\frac{3}{5}$).
点评 本题考查了正方形的性质,反比例函数与一次函数的交点问题,运用待定系数法求反比例函数与一次函数的解析式,三角形的面积,难度适中.运用方程思想是解题的关键.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案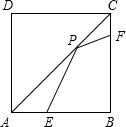 如图,正方形ABCD的边长为8,AE=3,CF=1,点P是对角线AC上一动点,则PE+PF的最小值4$\sqrt{5}$.
如图,正方形ABCD的边长为8,AE=3,CF=1,点P是对角线AC上一动点,则PE+PF的最小值4$\sqrt{5}$.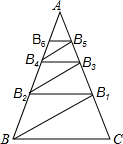 如图,△ABC中,AB=AC=1,∠ABC=72°,BB1平分∠ABC交AC于B1,过B1做B1B2∥BC交AB于B2,作B2B3平分∠AB2B1交AC于B3,过B3作B3B4∥BC交AB于B4,…则线段B1B2的长度为$\frac{3-\sqrt{5}}{2}$,线段B2n-1B2n的长度为($\frac{\sqrt{5}-1}{2}$)n-2.
如图,△ABC中,AB=AC=1,∠ABC=72°,BB1平分∠ABC交AC于B1,过B1做B1B2∥BC交AB于B2,作B2B3平分∠AB2B1交AC于B3,过B3作B3B4∥BC交AB于B4,…则线段B1B2的长度为$\frac{3-\sqrt{5}}{2}$,线段B2n-1B2n的长度为($\frac{\sqrt{5}-1}{2}$)n-2.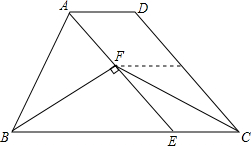 如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.
如图,在梯形ABCD中,AD∥BC,AB=CD,AE∥DC交BC于点E,BF⊥AE于F,AD=2,BC=7,CF=4,且∠ABF=∠DCF.