题目内容
9.点P是图①中三角形边上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )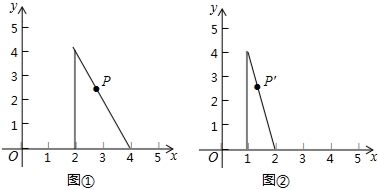
| A. | ($\frac{1}{2}$a,$\frac{1}{2}$b) | B. | ($\frac{1}{2}$a,b) | C. | (a-2,b) | D. | (a-1,b) |
分析 根据已知点坐标变化规律确定出P′坐标即可.
解答 解:根据题意得:(2,0)变化后的坐标为(1,0),(4,0)变化后的坐标为(2,0),
则P坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标($\frac{1}{2}$a,b),
故选B.
点评 此题考查了坐标与图形性质,弄清图中坐标变化是解本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案
相关题目
4.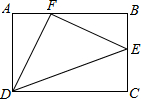 如图,在矩形ABCD中,E是BC的中点,连接DE,在AB上取一点F,连接DF,EF,恰有DF=EF.若∠DFE=90°,则sin∠EDC的值为( )
如图,在矩形ABCD中,E是BC的中点,连接DE,在AB上取一点F,连接DF,EF,恰有DF=EF.若∠DFE=90°,则sin∠EDC的值为( )
 如图,在矩形ABCD中,E是BC的中点,连接DE,在AB上取一点F,连接DF,EF,恰有DF=EF.若∠DFE=90°,则sin∠EDC的值为( )
如图,在矩形ABCD中,E是BC的中点,连接DE,在AB上取一点F,连接DF,EF,恰有DF=EF.若∠DFE=90°,则sin∠EDC的值为( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{6}}{6}$ | D. | $\frac{\sqrt{10}}{10}$ |
18.方程$\sqrt{x+1}$=5-x的解是( )
| A. | x=3 | B. | x=8 | C. | x1=3,x2=8 | D. | x1=3,x2=-8 |
 如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?
如图,A,B两处加工厂需从设在x轴上的C贷站和y轴上的D货站来回调运货物,当C,D建于何处时,AB+BC+CD+DA的路程最短?