题目内容
10.抛物线y=x2+ax+2与连接两点M(0,1)、N(2,3)的线段(包括M、N)有一个交点,求a的取值范围.分析 根据题意由x=2时,y<3,列出不等式即可解决问题.
解答 解:∵抛物线y=x2+ax+2与连接两点M(0,1)、N(2,3)的线段(包括M、N)有一个交点,
∴x=2时,y<3,即4+2a+2<3
解不等式得a<-$\frac{3}{2}$.
点评 本题考查二次函数的性质,理解题意是解图的关键,学会转化的思想,把问题转化为不等式解决,是中考常考题型.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.|1-tan45°|的值为( )
| A. | $\frac{1}{2}$ | B. | 1-$\frac{{\sqrt{2}}}{2}$ | C. | 1-$\frac{{\sqrt{3}}}{2}$ | D. | 0 |
9.点P是图①中三角形边上一点,坐标为(a,b),图①经过变化形成图②,则点P在图②中的对应点P′的坐标为( )
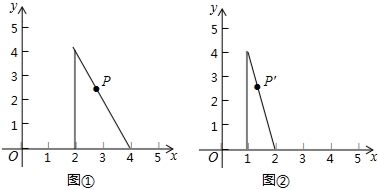

| A. | ($\frac{1}{2}$a,$\frac{1}{2}$b) | B. | ($\frac{1}{2}$a,b) | C. | (a-2,b) | D. | (a-1,b) |
10.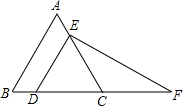 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
 如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )
如图,在等边三角形ABC中,点D,E分别在边BC,AC上,DE∥AB,过点E作EF⊥DE,交BC的延长线于点F;若△CEF一边的长为2,则△CEF的周长为( )| A. | 4+2$\sqrt{3}$ | B. | 4+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | C. | 2+2$\sqrt{3}$或2+$\frac{4}{3}$$\sqrt{3}$ | D. | 4+2$\sqrt{3}$或2+$\frac{2}{3}$$\sqrt{3}$ |
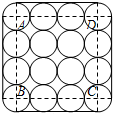 如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?
如图是一个组合烟花的横截面,其中16个圆的半径相同,点A、B、C、D分别是四个角上的圆的圆心,且四边形ABCD为正方形.若圆的半径为r,则组合烟花截面的周长和面积分别是多少?