题目内容
观察下列图形,并阅读图形下面的相关文字:

像这样有100条直线相交,最多交点的个数是 .

像这样有100条直线相交,最多交点的个数是
考点:直线、射线、线段
专题:规律型
分析:由于第一个图2条直线相交,最多有1个交点,第二个图3条直线相交最多有3个交点,第三个图4条直线相交,最多有6个,由此得到3=1+2,6=1+2+3,那么100条直线相交,最多有1+2+3+…+99=(1+99)×99÷2个,以此类推即可求解.
解答:解:∵第一个图2条直线相交,最多有1个交点,
第二个图3条直线相交最多有3个交点,
第三个图4条直线相交,最多有6个,
而3=1+2,6=1+2+3,
∴100条直线相交,最多交点的个数是1+2+3+…+99=(1+99)×99÷2=4950.
故答案为:4950.
第二个图3条直线相交最多有3个交点,
第三个图4条直线相交,最多有6个,
而3=1+2,6=1+2+3,
∴100条直线相交,最多交点的个数是1+2+3+…+99=(1+99)×99÷2=4950.
故答案为:4950.
点评:此题主要考查了平面内直线相交时交点个数的规律,解题时首先找出已知条件中隐含的规律,然后根据规律计算即可解决问题.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案
相关题目
现有五种说法:
①几个有理数相乘,当负因数有奇数个时,积为负;
②几个有理数相乘,积为负时,负因数有奇数个;
③当x<0时,|x|=-x;
④当|x|=-x时,x≤0.
⑤若|m|=3,|n|=7,且mn>0,则m+n=10.
其中正确的说法是( )
①几个有理数相乘,当负因数有奇数个时,积为负;
②几个有理数相乘,积为负时,负因数有奇数个;
③当x<0时,|x|=-x;
④当|x|=-x时,x≤0.
⑤若|m|=3,|n|=7,且mn>0,则m+n=10.
其中正确的说法是( )
| A、②③④ | B、③④⑤ |
| C、②③ | D、①②③④ |
下列名人中,①鲁迅、②姚明、③刘徽、④杨利伟、⑤高斯、⑥贝多芬、⑦陈景润、⑧祖冲之.其中是数学家的为( )
| A、①③⑤⑧ | B、③⑤⑦⑧ |
| C、②④⑥⑧ | D、④⑤⑥⑧ |
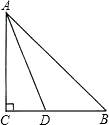 Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC,
Rt△ABC中,∠C=90°,∠B=45°,AD平分∠BAC, 某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面.
某居民小区的一处圆柱形的输水管道破裂,维修人员为更换管道,需要确定管道圆形截面的半径,如图是水平放置的破裂管道有水部分的截面. 如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=
如图,△ABC中,AD⊥BC,垂足是D.若BC=14,AD=12,tan∠BAD=