题目内容
2.写出在$\frac{1}{3}$和$\frac{4}{5}$之间,分母是15的所有的最简分数.$\frac{7}{15}、\frac{8}{15}、\frac{11}{15}$.分析 把$\frac{1}{3}$和$\frac{4}{5}$通分,化成分母是15的分数,然后把它们之间的分母是15的所有分数写出,把能继续约分的去掉,即可得解.
解答 解:因为$\frac{1}{3}$=$\frac{5}{15}$,$\frac{4}{5}$=$\frac{12}{15}$,
所以在$\frac{1}{3}$和$\frac{4}{5}$之间,分母是15的所有的分数有$\frac{6}{15}、\frac{7}{15}、\frac{8}{15}、\frac{9}{15}、\frac{10}{15}、\frac{11}{15}$,
其中$\frac{6}{15}、\frac{9}{15}、\frac{10}{15}$不是最简分数,
所以在$\frac{1}{3}$和$\frac{4}{5}$之间,分母是15的所有的最简分数为$\frac{7}{15}、\frac{8}{15}、\frac{11}{15}$,
故答案为:$\frac{7}{15}、\frac{8}{15}、\frac{11}{15}$.
点评 本题考查了有理数的除法,解决问题的关键是灵活应用约分和通分的知识来求解最简分数.

练习册系列答案
相关题目
3.若式子$\frac{\sqrt{x-1}}{x-2}$有意义,则x的取值范围是( )
| A. | x>1 | B. | x>1且x≠2 | C. | x≥1且x≠2 | D. | x≠2 |
7.4条直线两两相交,有( )个交点.
| A. | 1个 | B. | 4个 | C. | 6个 | D. | 以上都有可能 |

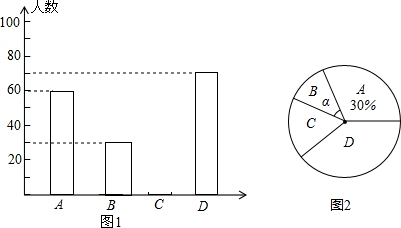
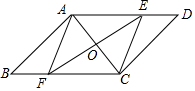 如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,
如图,在?ABCD中,对角线AC的垂直平分线EF与AC交于点O,与AD交于点E,与BC交于点F,连接EC,AF,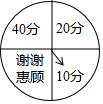 “五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.