题目内容
14．解不等式：|x-|2x+1||＞1．分析 分情况进行绝对值的化简，然后解不等式．
解答 解：不等式可化为：x-|2x+1|＞1或x-|2x+1|＜-1；
整理得：|2x+1|＜x-1或|2x+1|＞x+1，
由|2x+1|＜x-1可得$\left\{\begin{array}{l}{2x+1＞0}\\{2x+1＜x-1}\end{array}\right.$或$\left\{\begin{array}{l}{2x+1＜0}\\{-2x-1＜x+1}\end{array}\right.$，
无解；
由|2x+1|＞x+1可得$\left\{\begin{array}{l}{2x+1＞0}\\{2x+1＞x+1}\end{array}\right.$或$\left\{\begin{array}{l}{2x+1＜0}\\{-2x-1＞x+1}\end{array}\right.$，
解得x＞0或x＜-$\frac{2}{3}$，
故不等式的解集为：x＞0或x$＜-\frac{2}{3}$．
点评 本题考查了不等式的解法和绝对值的化简，解答本题的关键是根据x值的不同分情况进行绝对值的化简．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知方程组$\left\{\begin{array}{l}{ax-3y=5}\\{2x-by=1}\end{array}\right.$所对应的图象如图所示，试求出3a+7b的值．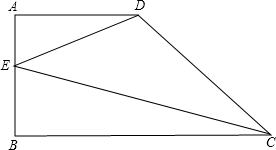
在直角梯形中，AB⊥BC，AD∥BC，BC＞AD，AD=3，AB=4，翻折△EBC至B与D重合，则tan∠BCE=$\frac{3}{4}$．
