题目内容
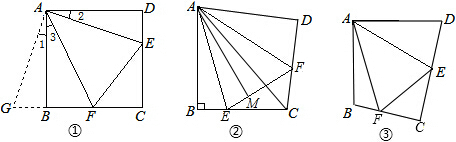
2.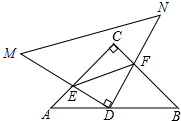 如图,将两个等腰直角三角形如图摆放,D为AB边的中点,E、F分别在腰AC、BC上(异于端点),当△MND绕着D点旋转时,设DE+DF=x,AB=10,△CEF的面积为y,则y与x之间的函数的图象大致为( )
如图,将两个等腰直角三角形如图摆放,D为AB边的中点,E、F分别在腰AC、BC上(异于端点),当△MND绕着D点旋转时,设DE+DF=x,AB=10,△CEF的面积为y,则y与x之间的函数的图象大致为( )| A. | 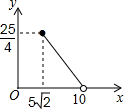 | B. | 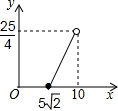 | C. | 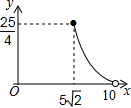 | D. | 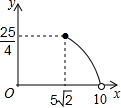 |
分析 连接CD,易证△CED≌△BFD,则四边形CEDF的面积=$\frac{1}{2}$×S△ACB,DE=DF,S△EDF=$\frac{1}{2}$×($\frac{1}{2}$x)2,于是△CEF的面积y=四边形CEDF的面积-S△EDF,根据函数关系式即可作出判断.
解答 解:连接CD,
∵△ABC是等腰直角三角形,D为AB边的中点,
∴∠ECD=∠B=45°,CD=BD,∠CDB=90°,
∵∠MDN=90°,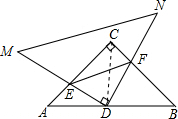
∴∠EDC=∠FDB,
在△CED和△BFD中,
$\left\{\begin{array}{l}{∠ECD=∠B}\\{CD=BD}\\{∠EDC=∠FDB}\end{array}\right.$,
∴△CED≌△BFD(ASA),
∴四边形CEDF的面积=$\frac{1}{2}$×S△ACB=S△CDB=$\frac{1}{2}$×BD2═$\frac{1}{2}$×52=$\frac{25}{2}$,DE=DF,
∵DE+DF=x,
∴S△EDF=$\frac{1}{2}$×($\frac{1}{2}$x)2=$\frac{1}{8}$x2
∴△CEF的面积y=四边形CEDF的面积-S△EDF$\frac{25}{2}$-$\frac{1}{8}$x2
故选:D.
点评 本题考查了动点问题的函数图象,证明△ADM≌△CDN,求出二次函数的解析式是解此题的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
3.下列说法中,正确的是( )
| A. | -a的绝对值等于a | |
| B. | 一个数的绝对值是它的相反数,则这个数一定是负数 | |
| C. | 若两个有理数的绝对值相等,则这两个数互为相反数 | |
| D. | 一个有理数的绝对值不小于它自身 |