题目内容
2.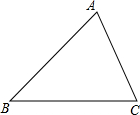 已知:如图在△ABC中,∠B=45°,∠C=60°,AB=6$\sqrt{2}$.求:
已知:如图在△ABC中,∠B=45°,∠C=60°,AB=6$\sqrt{2}$.求:(1)BC的长;
(2)△ABC的面积.
分析 (1)过点A作AD⊥BC,根据直角三角形的性质、勾股定理和等腰三角形的性质,可得出BD,AD,CD,即可得出答案;
(2)根据三角形的面积公式可得出△ABC的面积.
解答 解:(1)过点A作AD⊥BC,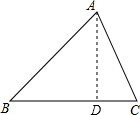 ∴∠ADB=90°,
∴∠ADB=90°,
∵∠B=45°,AB=6$\sqrt{2}$,
∴在Rt△ADB中,BD=AD=6$\sqrt{2}$×$\frac{\sqrt{2}}{2}$=6,
∵∠B=60°,
∴∠CAD=30°,
∴在Rt△ADB中,CD=$\frac{\sqrt{3}}{3}$AD=2$\sqrt{3}$,
∴BC=BD+CD=6+2$\sqrt{3}$;
(2)S=S△ABC=$\frac{1}{2}$BCBC•ADAD=$\frac{1}{2}$×(6+2$\sqrt{3}$)×6=18+6$\sqrt{3}$.
答:△ABC的面积是18+6$\sqrt{3}$.
点评 本题考查了勾股定理以及解直角三角形,还涉及到直角三角形的性质,30°的锐角所对的直角边等于斜边的一半.

练习册系列答案
 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案
相关题目
17.(a-b)2=( )
| A. | a2-2ab-b2 | B. | a2+2ab+b2 | C. | a2-b2 | D. | a2-2ab+b2 |
14.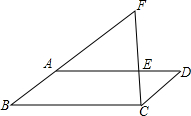 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )
 如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )
如图,在平行四边形ABCD中,点E在AD上,连接CE并延长与BA的延长线交于点F,若AE=2ED,S△CDE=3cm2,则△BCF的面积为( )| A. | 6cm2 | B. | 9cm2 | C. | 18cm2 | D. | 27cm2 |
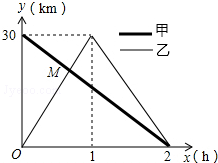 在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,下图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题:
在一条笔直的公路上有A,B两地,甲骑自行车从A地到B地,乙骑摩托车从B地到A地,到达A地后立即按原路返回,下图是甲、乙两人离B地的距离y(km)与行驶时间x(h)之间的函数图象,根据图象解答以下问题: