题目内容
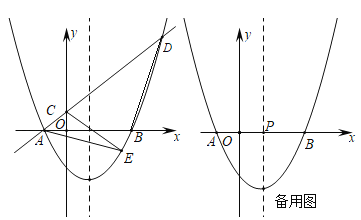
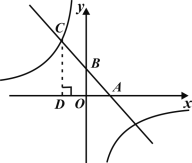
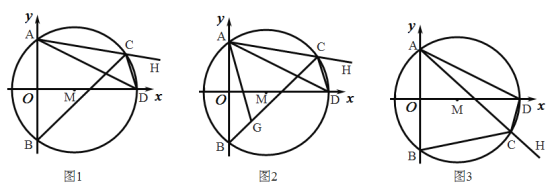
【题目】如图1,在平面直角坐标系中,已知![]() 的半径为5,圆心
的半径为5,圆心![]() 的坐标为
的坐标为![]() ,
,![]() 交
交![]() 轴于点
轴于点![]() ,交
,交![]() 轴于
轴于![]() ,
,![]() 两点,点
两点,点![]() 是
是![]() 上的一点(不与点
上的一点(不与点![]() 、
、![]() 、
、![]() 重合),连结
重合),连结![]() 并延长,连结
并延长,连结![]() ,
,![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)当点![]() 在
在![]() 上时.
上时.
①求证:![]() ;
;
②如图2,在![]() 上取一点
上取一点![]() ,使
,使![]() ,连结
,连结![]() .求证:
.求证:![]() ;
;
(3)如图3,当点![]() 在
在![]() 上运动的过程中,试探究
上运动的过程中,试探究![]() 的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
的值是否发生变化?若不变,请直接写出该定值;若变化,请说明理由.
【答案】(1)(0,4);(2)①详见解析;②详见解析;(3)不变,为![]() .
.
【解析】
(1)连结![]() ,在
,在![]() 中,
中,![]() 为圆的半径5,
为圆的半径5,![]() ,由勾股定理得
,由勾股定理得![]()
(2)①根据圆的基本性质及圆周角定理即可证明;
②根据等腰三角形的性质得到![]() ,根据三角形的外角定理得到
,根据三角形的外角定理得到![]() ,由①证明
,由①证明![]() 得到
得到![]() ,即可根据相似三角形的判定进行求解;
,即可根据相似三角形的判定进行求解;
(3)分别求出点C在B点时和点C为直径AC时,![]() 的值,即可比较求解.
的值,即可比较求解.
(1)连结![]() ,在
,在![]() 中,
中,![]() =5,
=5,![]() ,
,
∴![]()
∴A(0,4).
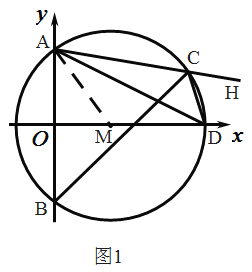
(2)连结![]() ,
,![]()
故![]() ,则
,则![]()
∵∠ABD+∠ACD=180°,∠HCD+∠ACD=180°,
∴![]()
∵![]() 与
与![]() 是弧
是弧![]() 所对的圆周角
所对的圆周角
∴![]() =
=![]()
又![]()
∴![]()
即![]()
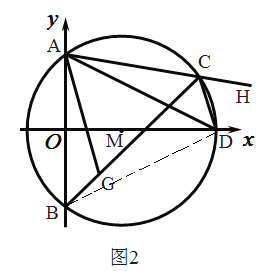
②∵![]()
∴![]()
∵![]() ,且由(2)得
,且由(2)得![]()
∴![]()
∴![]()
在![]() 与
与![]() 中
中
![]()
∴![]()
(3)①点C在B点时,如图,
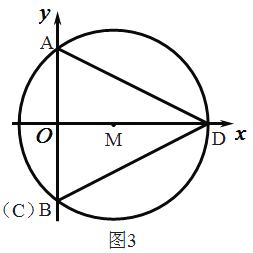
AC=2AO=8,BC=0,
CD=BD=![]()
∴![]() =
=![]() =
=![]() ;
;
当点C为直径AC与圆的交点时,如图
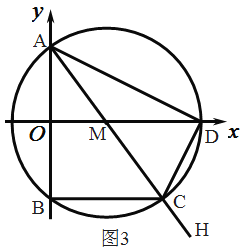
∴AC=2r=10
∵O,M分别是AB、AC中点,
∴BC=2OM=6,
∴C(6,-4)∵D(8,0)
∴CD=![]()
∴![]() =
=![]() =
=![]()
故![]() 的值不变,为
的值不变,为![]() .
.

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目