题目内容
【题目】如图,点![]() 是二次函数
是二次函数![]() 图像上的任意一点,点
图像上的任意一点,点![]() 在
在![]() 轴上.
轴上.
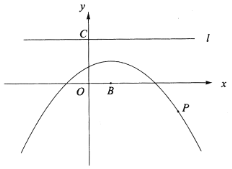
(1)以点![]() 为圆心,
为圆心,![]() 长为半径作
长为半径作![]() .
.
①直线![]() 经过点
经过点![]() 且与
且与![]() 轴平行,判断
轴平行,判断![]() 与直线
与直线![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
②若![]() 与
与![]() 轴相切,求出点
轴相切,求出点![]() 坐标;
坐标;
(2)![]() 、
、![]() 、
、![]() 是这条抛物线上的三点,若线段
是这条抛物线上的三点,若线段![]() 、
、![]() 、
、![]() 的长满足
的长满足![]() ,则称
,则称![]() 是
是![]() 、
、![]() 的和谐点,记做
的和谐点,记做![]() .已知
.已知![]() 、
、![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,直接写出
,直接写出![]() 的坐标_______.
的坐标_______.
【答案】(1)①![]() 与直线相切.理由见解析;②
与直线相切.理由见解析;②![]() 或
或![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①作直线![]() 的垂线,利用两点之间的距离公式及二次函数图象上点的特征证明线段相等即可;
的垂线,利用两点之间的距离公式及二次函数图象上点的特征证明线段相等即可;
②利用两点之间的距离公式及二次函数图象上点的特征构建方程即可求得答案.
(2)利用两点之间的距离公式分别求得各线段的长,根据“和谐点”的定义及二次函数图象上点的特征构建方程即可求得答案.
(1)①![]() 与直线相切.
与直线相切.
如图,过![]() 作
作![]() 直线
直线![]() ,垂足为
,垂足为![]() ,设
,设![]() .
.
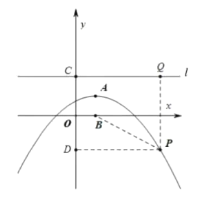
则![]() ,
,![]()
![]() ,即:
,即:![]()
![]()
![]()
![]() 与直线
与直线![]() 相切.
相切.
②当![]() 与
与![]() 轴相切时
轴相切时![]()
∴![]() ,
,
![]() ,即:
,即:![]()
代入![]()
化简得:![]() 或
或![]() .
.
解得:![]() ,
,![]() .
.
![]() 或
或![]() .
.
(2)已知![]() 、
、![]() 的横坐标分别是
的横坐标分别是![]() ,
,![]() ,代入二次函数的解析式得:
,代入二次函数的解析式得:
![]() ,
,![]() ,
,
设![]() ,
,
∵点B的坐标为![]() ,
,![]()
∴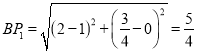 ,
,
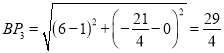 ,
,
![]() ,
,
依题意得:![]() ,即
,即![]() ,
,
![]() ,即:
,即:![]() ,
,
∴![]() (不合题意,舍去)或
(不合题意,舍去)或![]() ,
,
把![]() ,代入
,代入![]() 得:
得:
![]()
直接开平方解得:![]() ,
,![]() ,
,
∴![]() 的坐标为:
的坐标为:![]() 或
或![]()

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目