题目内容
1．先化简，再求值：$\frac{a+2}{a+3}$÷$\frac{{a}^{2}-4}{{a}^{2}+3a}$-1，其中a=$\frac{1}{2}$．分析 先把分子分母因式分解，再把除法运算化为乘法运算，然后约分得到原式=$\frac{2}{a-2}$，再把a的值代入计算即可．
解答 解：原式═$\frac{a+2}{a+3}$÷$\frac{（a+2）（a-2）}{a（a+3）}$-1
=$\frac{a+2}{a+3}$•$\frac{a（a+3）}{（a+2）（a-2）}$-1
=$\frac{a}{a-2}$-$\frac{a-2}{a-2}$
=$\frac{2}{a-2}$，
当a=$\frac{1}{2}$时，原式=$\frac{2}{\frac{1}{2}-2}$=-$\frac{4}{3}$．
点评 本题考查了分式的化简求值：先把分式化简后，再把分式中未知数对应的值代入求出分式的值．在化简的过程中要注意运算顺序和分式的化简．化简的最后结果分子、分母要进行约分，注意运算的结果要化成最简分式或整式．
练习册系列答案
优学名师名题系列答案
相关题目
9．某班50名同学用目测的方法估计一本书的长度（单位：cm），将估测数据进行分组整理，结果如下表：
利用这50个数据的平均数估计这本书的长度．
| 估测值x/cm | 16≤x＜20 | 20≤x＜24 | 24≤x＜28 | 28≤x≤32 | 合计 |
| 数据个数 | 6 | 19 | 17 | 8 | 9 |
16．已知空气的单位体积质量是0.001239g/cm3，则用科学记数法表示该数为（ ）g/cm3．
| A． | 1.239×10-3 | B． | 1.2×10-3 | C． | 1.239×10-2 | D． | 1.239×10-4 |
6．
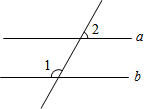如图，已知a∥b，∠1=115°，则∠2的度数是（ ）
如图，已知a∥b，∠1=115°，则∠2的度数是（ ）| A． | 45° | B． | 55° | C． | 65° | D． | 85° |
已知关于x的一元二次方程x2$+2x+\frac{k-1}{2}=0$有两个不相等的实数根，k为正整数．