题目内容
2.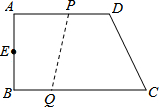 已知:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/秒的速度移动,点Q从点C开始沿CB边向点B以2cm/秒的速度移动.如果P、Q分别从A、C同时出发.设移动的时间为t.
已知:如图,在梯形ABCD中,AD∥BC,∠B=90°,AB=14cm,AD=18cm,BC=21cm,点P从点A开始沿AD边向点D以1cm/秒的速度移动,点Q从点C开始沿CB边向点B以2cm/秒的速度移动.如果P、Q分别从A、C同时出发.设移动的时间为t.求:(1)t为何值时,梯形PQCD是等腰梯形;
(2)t为何值时,AB的中点E到线段PQ的距离为7cm.
分析 (1)过P作PN⊥BC于N,过D作DM⊥BC于M,先证明四边形ABMD是矩形,从而得到AD=BM,再根据边与边之间的关系,列一元一次方程3t-21=3,得到t=8,即t=8秒时,梯形PQCD是等腰梯形;
(2)在Rt△PQM中,表示出PM=14,QM=3t-1,然后根据PM2+QM2=PQ2,得到142+(3t-21)2=(21-t)2,求得t值即可.
解答 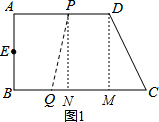 解:如图1,过P作PN⊥BC于N,过D作DM⊥BC于M,
解:如图1,过P作PN⊥BC于N,过D作DM⊥BC于M,
∵AD∥BC,∠B=90°,DM⊥BC,
∴四边形ABMD是矩形,AD=BM.
∴MC=BC-BM=BC-AD=3.
又∵QN=BN-BQ=AP-BQ=t-(21-2t)=3t-21.
若梯形PQCD为等腰梯形,则QN=MC=3.
得3t-21=3,t=8,
即t=8秒时,梯形PQCD是等腰梯形.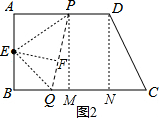
(2)如图2,过E作EF⊥PQ于F,连接PE,EQ,当EF=7cm时,
∵AE=BE=$\frac{1}{2}$AB=$\frac{1}{2}$×14=7cm,
∴AE=EF=BE,
∵AD∥BC,∠B=90°,
∴∠A=90°,
∵PE=PE,EQ=EQ,
∴△AEP≌△FEP,△BEQ≌△FEQ,
∴PA=PF=t,BQ=FQ=21-2t,
∴PQ=PF+FQ=21-t,
在Rt△PQM中,PM=14,QM=3t-1,
∵PM2+QM2=PQ2,
∴142+(3t-21)2=(21-t)2,
解得:t=3.5或t=7,
∴当t为3.5或7时,AB的中点E到线段PQ的距离为7cm.
点评 此题主要考查了等腰梯形以及直角梯形和平行四边形的判定与性质,熟练掌握它们的定义是解题关键.

练习册系列答案
相关题目
 如图,∠AOB=90°,OD平分∠BOC,∠DOE=45°,则∠AOE=∠COE(填“<”“>”或“=”号)
如图,∠AOB=90°,OD平分∠BOC,∠DOE=45°,则∠AOE=∠COE(填“<”“>”或“=”号) 如图,在∠AOB内找一点P,使得点P到∠AOB的两边距离相等,且使点P到点C的距离最短(尺规作图,请保留作图痕迹).
如图,在∠AOB内找一点P,使得点P到∠AOB的两边距离相等,且使点P到点C的距离最短(尺规作图,请保留作图痕迹).
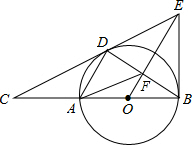 如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.
如图,点D是半径为5的⊙O上一点,点C在直径BA的延长线上,且∠CDA=∠CBD,CA=8,过点B作⊙O的切线BE交直线CD于点E,连接AD、BD、OE的交点是F,连接AF.