题目内容
已知:如图1,O为正方形ABCD的中心,E为OD延长线上一点,EF∥AD交CA的延长线于点F.
(1)求证:AF=DE;
(2)如图2,将图1中的△EOF绕点O逆时针旋转角α得到△E1OF1.
①探究AF1与DE1的数量关系,并给予证明;
②若当α=30°时,E1F1恰好经过点A,则
= .
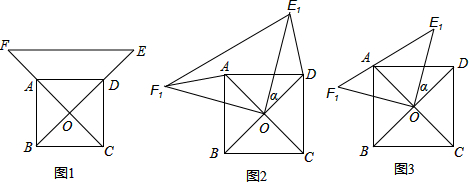
(1)求证:AF=DE;
(2)如图2,将图1中的△EOF绕点O逆时针旋转角α得到△E1OF1.
①探究AF1与DE1的数量关系,并给予证明;
②若当α=30°时,E1F1恰好经过点A,则
| S△OE1F1 |
| S正ABCD |

考点:正方形的性质,全等三角形的判定与性质
专题:
分析:(1)应用平行线平分线段定理可求得
=
,根据OA=OD可求得AF=DE;
(2)①由△EOF绕点O逆时针旋转角α可知OA=OD,OE1=OF1,∠AOF1=∠DOE1求得三角形全等,从而求得AF1=AE1.
②依据三角形的面积等于两个分割的三角形面积的和,求得
=
,再根据三角形相似△E1OF1∽△AOD面积的比等于相似比的平方,从而求得.
| OA |
| OF |
| OD |
| OE |
(2)①由△EOF绕点O逆时针旋转角α可知OA=OD,OE1=OF1,∠AOF1=∠DOE1求得三角形全等,从而求得AF1=AE1.
②依据三角形的面积等于两个分割的三角形面积的和,求得
| a |
| b |
1+
| ||
| 2 |
解答:(1)证明:∵EF∥AD
∴
=
∵OA=OD,
∴OF=OE,
∴OF-OA=OE-OD,
∴AF=AE.
(2)①AF1=DE1
证明:∵OF=OE,
∴OF1=OE1,
在△AOF1与△DOE1中
∴△AOF1≌△DOE1(SAS),
∴AF1=DE1,
②设OE1=OF1=a,OA=OD=b
∴S △AOF1=
×sih30°ba=
ab,
S △AOE1=
×sin60°ba=
ab.
∴S △E1OF1=S △AOF1+S △AOE1=(
)ab
∵S △E1OF1=
a2
∴(
)ab=
a2
解得
=
∵△E1OF1与△AOD都是等腰直角三角形;
∴△E1OF1∽△AOD
∴
=(
)2=(
)2=
∴
=
=
×(
)=
.
∴
| OA |
| OF |
| OD |
| OE |
∵OA=OD,
∴OF=OE,
∴OF-OA=OE-OD,
∴AF=AE.
(2)①AF1=DE1
证明:∵OF=OE,
∴OF1=OE1,
在△AOF1与△DOE1中
|
∴△AOF1≌△DOE1(SAS),
∴AF1=DE1,
②设OE1=OF1=a,OA=OD=b
∴S △AOF1=
| 1 |
| 2 |
| 1 |
| 4 |
S △AOE1=
| 1 |
| 2 |
| ||
| 4 |
∴S △E1OF1=S △AOF1+S △AOE1=(
1+
| ||
| 4 |
∵S △E1OF1=
| 1 |
| 2 |
∴(
1+
| ||
| 4 |
| 1 |
| 2 |
解得
| a |
| b |
1+
| ||
| 2 |
∵△E1OF1与△AOD都是等腰直角三角形;
∴△E1OF1∽△AOD
∴
| S△E1OF1 |
| S△AOD |
| a |
| b |
1+
| ||
| 2 |
2+
| ||
| 2 |
∴
| S△OE1F1 |
| S正ABCD |
| S△OE1F1 |
| 4S△AOD |
| 1 |
| 4 |
2+
| ||
| 2 |
2+
| ||
| 8 |
点评:本题考查平行线的性质,全等三角形的判定以及相似三角形的判定和性质,以及图形分割的问题.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案
相关题目
 如图,AB∥CD,AC与BD相交于点O,AB=3,若BO:BD=1:3,则CD等于
如图,AB∥CD,AC与BD相交于点O,AB=3,若BO:BD=1:3,则CD等于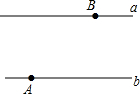
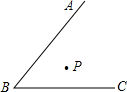 如图,点P是∠ABC内一点,
如图,点P是∠ABC内一点,