题目内容
如果将抛物线y=x2+3沿x轴向右平移2个单位，那么所得新的抛物线的表达式是 ．
考点：二次函数图象与几何变换
专题：
分析：易得原抛物线的顶点及平移后新抛物线的顶点，利用顶点式根据平移不改变二次项系数可得新抛物线解析式．
解答：解：∵抛物线y=x2+3的顶点为（0，3），
∴向右平移2个单位得到的顶点为（2，3），
∴把抛物线y=x2+3向右平移2个单位，所得抛物线的表达式为y=（x-2）2+3．
故答案为y=（x-2）2+3．
∴向右平移2个单位得到的顶点为（2，3），
∴把抛物线y=x2+3向右平移2个单位，所得抛物线的表达式为y=（x-2）2+3．
故答案为y=（x-2）2+3．
点评：本题考查二次函数图象与几何变换．用到的知识点为：二次函数的平移不改变二次项的系数；关键是根据左右平移只改变二次函数的顶点的横坐标得到新抛物线的顶点．
练习册系列答案
相关题目
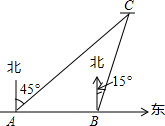2014年3月8日凌晨，马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失，至今没有被发现踪迹．飞机上有239名乘客，其中154名是中国同胞．中国政府启动了全面应急和搜救机制，派出多艘中国舰船在相关海域进行搜救．如图，某日在南印度洋海域有两艘自西向东航行的搜救船A，B，B船在A船的正东方向，且两船保持20海里的距离，某一时刻两船同时测得在A的东北方向，B的北偏东15°方向有疑似物C，求此时疑似物C与搜救船A，B的距离各是多少（结果保留根号）
如图，点A在双曲线y=