题目内容
18.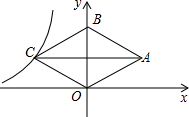 如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )
如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数y=$\frac{k}{x}$(x<0)的图象经过点C,则k的值为( )| A. | -12 | B. | -6 | C. | 6 | D. | 12 |
分析 设菱形的两条对角线相交于点D,如图,根据菱形的性质得OB⊥AC,BD=OD=2,CD=AD=3,再由菱形ABCD的对角线OB在y轴上得到AC∥x轴,则可确定C(-3,2),然后根据反比例函数图象上点的坐标特征求k的值.
解答  解:设菱形的两条对角线相交于点D,如图,
解:设菱形的两条对角线相交于点D,如图,
∵四边形ABCD为菱形,
∴OB⊥AC,BD=OD=2,CD=AD=3,
∵菱形ABCO的对角线OB在y轴上,
∴AC∥x轴,
∴C(-3,2),
∴k=-3×2=-6.
故选B.
点评 本题考查了反比例函数图象上点的坐标特征:反比例函数y=$\frac{k}{x}$(k为常数,k≠0)的图象是双曲线,图象上的点(x,y)的横纵坐标的积是定值k,即xy=k.也考查了菱形的性质.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目
8.以下列线段为三边,不能构成直角三角形的是( )
| A. | a=$\sqrt{3}$,b=$\sqrt{4}$,c=$\sqrt{5}$ | B. | a=1,b=$\sqrt{2}$,c=$\sqrt{3}$ | C. | a=5,b=12,c=13 | D. | a=15,b=17,c=8 |

 如图是由5个大小相同的正方形组成的几何体,它的主视图是( )
如图是由5个大小相同的正方形组成的几何体,它的主视图是( )



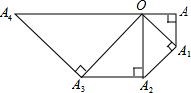 如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.
如图,在等腰Rt△OAA1中,∠OAA1=90°,OA=1,以OA1为直角边作等腰Rt△OA1A2,以OA2为直角边作等腰Rt△OA2A3,…,则OA10的长度为32.