题目内容
19．抛物线y=x2-2x-3与x轴的交点个数是（ ）| A． | 0个 | B． | 1个 | C． | 2个 | D． | 3个 |
分析 通过解方程x2-2x-3=0可得到抛物线与x轴的交点坐标，于是可判断抛物线y=-x2+3x-2与x轴的交点个数．
解答 解：当y=0时，x2-2x-3=0，解得x1=-1，x2=3．
则抛物线与x轴的交点坐标为（-1，0），（3，0）．
故选C．
点评 本题考查了抛物线与x轴的交点：把求二次函数y=ax2+bx+c（a，b，c是常数，a≠0）与x轴的交点坐标问题转化为解关于x的一元二次方程．
练习册系列答案
相关题目
9．
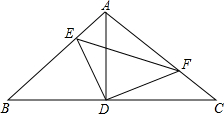如图，Rt△ABC中，∠BAC=90°，AB=AC，点D为BC的中点，点E、F分别在边AB和边AC上，且∠EDF=90°，则下列结论不一定成立的是（ ）
如图，Rt△ABC中，∠BAC=90°，AB=AC，点D为BC的中点，点E、F分别在边AB和边AC上，且∠EDF=90°，则下列结论不一定成立的是（ ）| A． | △ADF≌△BDE | B． | S四边形AEDF=$\frac{1}{2}$S△ABC | ||
| C． | BE+CF=$\sqrt{2}$AD | D． | EF=AD |
10．在-12，|-5|，-（-4），-|0|中，正数共有（ ）
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
7．下列的数中，是负数的是（ ）
| A． | +7 | B． | -2.3 | C． | 0.53 | D． | 0 |
4．在△ABC中，若cosA=$\frac{\sqrt{2}}{2}$，tanB=$\sqrt{3}$，则这个三角形一定是（ ）
| A． | 直角三角形 | B． | 等腰三角形 | C． | 钝角三角形 | D． | 锐角三角形 |
11．
如图，在△ABC中，∠B=90°，∠A=60°，AB=4，则AC的长度为（ ）
如图，在△ABC中，∠B=90°，∠A=60°，AB=4，则AC的长度为（ ）| A． | 4 | B． | 6 | C． | 8 | D． | 10 |
如图，在四边形ABCD中，∠B=90°，DE∥AB，交BC于E，交AC于F，DE=BC，∠CDE=∠ACB=30°．