题目内容
6.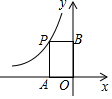 反比例函数y=-$\frac{3}{x}$(x<0)如图所示,则矩形OAPB的面积是( )
反比例函数y=-$\frac{3}{x}$(x<0)如图所示,则矩形OAPB的面积是( )| A. | 3 | B. | -3 | C. | $\frac{3}{2}$ | D. | -$\frac{3}{2}$ |
分析 可设出点P的坐标,则可表示出矩形OAPB的面积.
解答 解:
∵点P在反比例函数y=-$\frac{3}{x}$(x<0)的图象上,
∴可设P(x,-$\frac{3}{x}$),
∴OA=-x,PA=-$\frac{3}{x}$,
∴S矩形OAPB=OA•PA=-x•(-$\frac{3}{x}$)=3,
故选A.
点评 本题主要考查反比例函数上点的坐标特征,利用P点坐标表示出矩形OAPB的面积是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.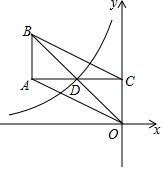 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
 如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )
如图,双曲线y=-$\frac{3}{2x}$(x<0)经过?ABCO的对角线交点D,已知边OC在y轴上,且AC⊥OC于点C,则?OABC的面积是( )| A. | $\frac{3}{2}$ | B. | $\frac{9}{4}$ | C. | 3 | D. | 6 |
11.若(x+2)(x-1)=x2+mx+n成立,则m+n的值为( )
| A. | 1 | B. | -2 | C. | -1 | D. | 2 |
18. 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
(1)填写表中的空格;
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
 下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.
下面是一组同学做“抛掷质地均匀的硬币试验”获得的数据.| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的 频数m | 51 | 98 | 153 | 200 | 250 |
| 正面朝上的 频率mn | 0.51 | 0.49 | 0.51 | 0.50 | 0.51 |
(2)画出折线统计图;
(3)抛掷质地均匀的硬币,正面朝上的概率的估计值是多少?
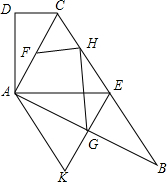 如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.
如图,在四边形ABCD中,AC平分∠BCD,AC2=CD•BC,E是BC的中点,AC⊥AB.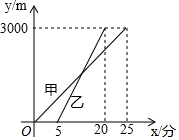 赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题:
赛龙舟是端午节的主要习俗,某市甲乙两支龙舟队在端午节期间进行划龙舟比赛,从起点A驶向终点B,在整个行程中,龙舟离开起点的距离y(米)与时间x(分钟)的对应关系如图所示,请结合图象解答下列问题: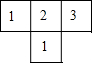 如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )
如图是由几个大小相同的小正方体搭成的几何体的俯视图,小正方体中的数字表示该位置小正方体的个数,则该几何体的正视图是( )