题目内容
9.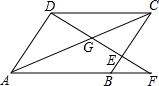 如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3
如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3(1)若DC=12,求BF的长;
(2)求DG:GF.
分析 (1)在平行四边形ABCD中,由BE:AD=1:3,得到BE:CE=1:2,通过△CDE∽△BFE,于是得到$\frac{CD}{BF}=\frac{CE}{BE}=\frac{2}{1}$,即可得到结论;
(2)由△CEG∽△ADG,得到$\frac{CE}{AD}=\frac{CG}{AG}$=$\frac{2}{3}$,通过△CDG∽△AGF,根据相似三角形的性质即可得到结论.
解答 解:(1)在平行四边形ABCD中,
∵AD=BC,AB=CD,AB∥CD,
∵BE:AD=1:3,
∴BE:CE=1:2,
∵CD∥BF,
∴△CDE∽△BFE,
∴$\frac{CD}{BF}=\frac{CE}{BE}=\frac{2}{1}$,
∵DC=12,
∴BF=6;
(2)∵AD∥BC,
∴△CEG∽△ADG,
∴$\frac{CE}{AD}=\frac{CG}{AG}$=$\frac{2}{3}$,
∵CD∥AF,
∴$\frac{DG}{GF}=\frac{CG}{AG}$=$\frac{2}{3}$.
点评 本题考查了相似三角形的判定和性质,平行四边形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

练习册系列答案
相关题目
14.若关于x的一元二次方程ax2+bx+5=0(a≠0)的解是x=1,则2015-a-b的值是( )
| A. | 2017 | B. | 2018 | C. | 2019 | D. | 2020 |
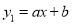 与
与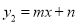 相交于点
相交于点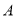 (2,
(2, 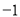 ),若
),若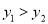 ,则
,则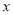 的取值范围是( )
的取值范围是( )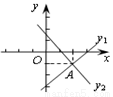
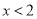 B.
B. 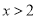 C.
C. 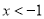 D.
D. 
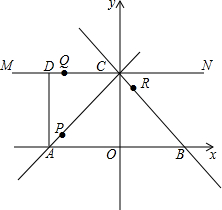 如图,在直角坐标系中,已知点A、B、C是坐标轴上的点,直线AC:y=x+3,直线BC:y=-x+3,直线MN过点C且与x轴平行,AD⊥MN,垂足为D.点 P、Q、R分别从A、D、C出发分别沿AC、DN、CB方向运动,点P、点R的运动速度都为1个单位长度/秒,点Q的运动速度都为$\sqrt{2}$个单位长度/秒.
如图,在直角坐标系中,已知点A、B、C是坐标轴上的点,直线AC:y=x+3,直线BC:y=-x+3,直线MN过点C且与x轴平行,AD⊥MN,垂足为D.点 P、Q、R分别从A、D、C出发分别沿AC、DN、CB方向运动,点P、点R的运动速度都为1个单位长度/秒,点Q的运动速度都为$\sqrt{2}$个单位长度/秒.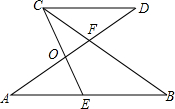 如图,已知AB∥CD,AD与BC交于点F,AF=BF,点E在AB上,CE与AD交于点O,EC=EB,OF=4,FD=5,OE:OC=2:3.
如图,已知AB∥CD,AD与BC交于点F,AF=BF,点E在AB上,CE与AD交于点O,EC=EB,OF=4,FD=5,OE:OC=2:3.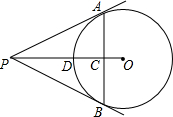 如图,PA、PB切⊙O于点A、B,PO与AB交于点C,PO交⊙O于点D,且PA=8,PO=10,则OC=$\frac{18}{5}$.
如图,PA、PB切⊙O于点A、B,PO与AB交于点C,PO交⊙O于点D,且PA=8,PO=10,则OC=$\frac{18}{5}$.