题目内容
5.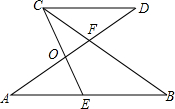 如图,已知AB∥CD,AD与BC交于点F,AF=BF,点E在AB上,CE与AD交于点O,EC=EB,OF=4,FD=5,OE:OC=2:3.
如图,已知AB∥CD,AD与BC交于点F,AF=BF,点E在AB上,CE与AD交于点O,EC=EB,OF=4,FD=5,OE:OC=2:3.(1)求证:OC2=OF•OD;
(2)求CD的长;
(3)求S△OCF:S△ABF的值.
分析 (1)由等腰三角形的性质得到∠A=∠B,根据平行线的性质得到∠D=∠A,等量代换得到∠D=∠OCF,推出△COF∽△CDO,即可得到结论.
(2)由CD∥AB,得到∠D=∠A,∠DCF=∠B,等量代换得到∠D=∠DCF,于是得到CF=DF=5,求得OC=6,由△COF∽△CDO,列比例式即可得到结论;
(3)由已知条件得到OE=4,于是得到BE=CE=10,由△CDO△AEO,得到$\frac{CD}{AE}=\frac{OC}{OE}$=$\frac{3}{2}$,通过△CDF∽△ABF,得到$\frac{{S}_{△CDF}}{{S}_{△ABF}}$=($\frac{CD}{AB}$)2=$\frac{1}{4}$,于是求得S△CDF=$\frac{1}{4}$S△ABF,由于$\frac{{S}_{△COF}}{{S}_{△CDF}}$=$\frac{OF}{DF}$=$\frac{4}{5}$,于是得到S△COD=$\frac{4}{5}$S△CDF=$\frac{1}{5}$S△ABF,即可得到结论.
解答 (1)证明:∵AF=BF,
∴∠A=∠B,
∵AB∥CD,
∴∠D=∠A,
∴∠D=∠B,
∵EC=EB,
∴∠B=∠ECB,
∴∠D=∠OCF,
∵∠COF=∠COD,
∴△COF∽△CDO,
∴$\frac{OC}{OD}=\frac{OF}{OC}$,
∴OC2=OF•OD;
(2)解:∵CD∥AB,
∴∠D=∠A,∠DCF=∠B,
∵∠A=∠B,
∴∠D=∠DCF,
∴CF=DF=5,
∵OC2=OF•OD,
∴OC2=4×(4+5)=36,
∴OC=6,
∵△COF∽△CDO,
∴$\frac{OC}{OF}=\frac{CD}{CF}$,
∴$\frac{6}{4}=\frac{CD}{5}$,
∴CD=$\frac{15}{2}$;
(3)解:∵OE:OC=2:3,OC=6,
∴OE=4,
∴BE=CE=10,
∵CD∥AE,
∴△CDO∽△AEO,
∴$\frac{CD}{AE}=\frac{OC}{OE}$=$\frac{3}{2}$,
∴AE=5,
∴AB=15,
∵CD∥AB,
∴△CDF∽△ABF,
∴$\frac{{S}_{△CDF}}{{S}_{△ABF}}$=($\frac{CD}{AB}$)2=$\frac{1}{4}$,
∴S△CDF=$\frac{1}{4}$S△ABF,
∵$\frac{{S}_{△COF}}{{S}_{△CDF}}$=$\frac{OF}{DF}$=$\frac{4}{5}$,
∴S△COD=$\frac{4}{5}$S△CDF=$\frac{1}{5}$S△ABF,
∴S△OCF:S△ABF=$\frac{1}{5}$.
点评 本题考查了相似三角形的判定和性质,平行线的性质,等腰三角形的性质,熟练掌握相似三角形的判定和性质是解题的关键.

| 与标准质量的差值/克 | -5 | -2 | 0 | 1 | 3 | 6 |
| 袋数 | 4 | 3 | 6 | 3 | 3 | 1 |
(2)若标准质量为450克,则抽样检测的总质量是多少克?
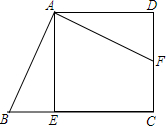 如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )
如图,在四边形ABCD中,AD∥BC,∠C=90°,点E,F分别在BC,CD上,若△ADF≌△AEB,则下列说法中不正确的是( )| A. | DF=EB | B. | AE⊥BC | C. | ∠DAF=∠EAB | D. | AB=AD |
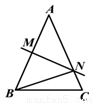

 如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.
如图,正方形ABCD的边长为5,以A为原点,AB所在的直线为x轴建立平面直角坐标系,在图中画出y轴,并写出A、B、C、D四个顶点的坐标.
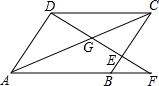 如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3
如图,在平行四边形ABCD中,点E在边BC上,DE的延长线交AB的延长线于点F,AC与DF交于G,BE:AD=1:3