题目内容
20．作图题：（1）作下面钝角△ABC三边上的高．
（2）把下面三角形面积分四等分（至少三种方法）
分析 （1））以C为圆心，适当的长为半径画弧，交AB于两点，再分别以这两点为圆心，大于它们的一半长为半径画弧，两弧交于一点，再过C点和这个交点画线可得CD⊥AB，利用同法作BF⊥AC，AE⊥BC即可．
（2）根据高一定时，三角形的面积与底成正比例的性质可得：三角形的中线把三角形分成面积相等的两个三角形，先分成两个面积相等的三角形，进而继续即可，或者连接三角形的三条中位线，也可以把三角形分成面积相等的四部分．据此即可解答．
解答 解：（1）如图所示：
；
（2）如图所示：
．
点评 此题主要考查了复杂作图，关键是掌握三角形的高，以及三角形的中线平分三角形的面积．
练习册系列答案
寒假天地重庆出版社系列答案
相关题目
13．如果式子$\sqrt{{{（x-3）}^2}}-|{x-2}|$化简的结果为5-2x，则x的取值范围是（ ）
| A． | x≥3 | B． | x≤2 | C． | x≥2 | D． | 2≤x≤3 |
如图，在△ABC中，AB=AC，AD是角平分线，点E在AD上，请写出图中两对全等三角形，并选择其中的一对加以证明．
15．下列计算正确的是（ ）
| A． | a8÷a2=a4 | B． | a3•a2=a6 | C． | （a3）2=a6 | D． | a+2a2=3a2 |
5．化简$\sqrt{-{x}^{3}}$-x$\sqrt{-\frac{1}{x}}$，得（ ）
| A． | （x-1 ）$\sqrt{-x}$ | B． | （1-x ）$\sqrt{-x}$ | C． | -（x+1 ）$\sqrt{x}$ | D． | （x-1 ） $\sqrt{x}$ |
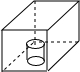如图，向放在水槽底部的烧杯注水（流量一定），注满烧杯后，继续注水，直至注满水槽．水槽中水面上升高度h与注水时间的关系大致是下列图象中的（ ）
如图，FG⊥AB，∠AED=∠ACB，∠1=∠2，试说明CD⊥AB．