题目内容
13．如果式子$\sqrt{{{（x-3）}^2}}-|{x-2}|$化简的结果为5-2x，则x的取值范围是（ ）| A． | x≥3 | B． | x≤2 | C． | x≥2 | D． | 2≤x≤3 |
分析 根据算术平方根的被开方数是非负数，绝对值是非负数，化简求解即可．
解答 解：∵$\sqrt{{（x-3）}^{2}}$-|x-2|化简的结果为5-2x，
∴$\sqrt{{（x-3）}^{2}}$-|x-2|=3-x+2-x=5-2x，
∴x-3≤0，x-2≥0，
∴2≤x≤3．
故选D．
点评 本题考查了二次根式的性质与化简，解答本题的关键在于熟练掌握二次根式的性质．
练习册系列答案
怎样学好牛津英语系列答案
导学教程高中新课标系列答案
相关题目
4．下列计算中，正确的是 （ ）
| A． | $\sqrt{5}-\sqrt{3}=\sqrt{2}$ | B． | $2+\sqrt{3}=2\sqrt{3}$ | C． | $\sqrt{8}×\sqrt{2}=4$ | D． | $\frac{{\sqrt{10}}}{2}=\sqrt{5}$ |
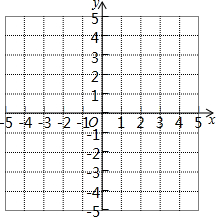在平面直角坐标系中，点O为坐标原点，已知点A（2，0）和点B（2，2），请画出△OAB以及一个以点O为位似中心的△OAB的位似图形△OA'B'，使△OAB与△OA'B'的相似比为1：2．
