题目内容
2.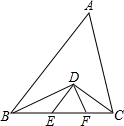 如图所示,在△ABC中,∠ABC和∠ACB的角平分线相交于D,过点D作DE∥AB交BC于点E,DF∥AC交BC于点F.若BC=15,AB=16,AC=12,则△DEF的周长为15.
如图所示,在△ABC中,∠ABC和∠ACB的角平分线相交于D,过点D作DE∥AB交BC于点E,DF∥AC交BC于点F.若BC=15,AB=16,AC=12,则△DEF的周长为15.
分析 根据角平分线的定义可得∠ABD=∠EBD,再根据两直线平行,内错角相等可得∠ABD=∠EDB,然后求出∠EBD=∠EDB,根据等角对等边的性质可得BE=DE,同理可得CF=DF,然后求出△DEF的周长=BC,代入数据即可得解.
解答 解:∵BD平分∠ABC,
∴∠ABD=∠EBD,
∵DE∥AB,
∴∠ABD=∠EDB,
∴∠EBD=∠EDB,
∴BE=DE,
同理可得:CF=DF,
∴△DEF的周长=DE+EF+DF=BE+EF+CF=BC,
∵BC=15,
∴△DEF的周长=15.
故答案为:15.
点评 本题考查了等腰三角形的性质与判定,主要利用了角平分线的定义,平行线的性质,等角对等边的性质,是基础题,熟记性质是解题的关键.

练习册系列答案
相关题目
13.下列各式中,运算正确的是( )
| A. | 2x2-x=x2 | B. | (x2)3=x5 | C. | 2$\sqrt{3}+3\sqrt{3}=5\sqrt{3}$ | D. | x2•x3=x6 |
10.在平面直角坐标系中,反比例函数y=$\frac{{a}^{2}-a+1}{x}$图象的两个分支分别在( )
| A. | 第一、二象限 | B. | 第三、四象限 | C. | 第二、四象限 | D. | 第一、三象限 |
17.兰州市某校为了解七年级学生课堂发言情况,随机抽取该年级一个班,对该班学生某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人的比为5:2,请结合图中相关数据回答下列问题:

(1)求出抽取的该班人数,并补全直方图.
(2)该年级共有学生600人,请估计全年级在这天里发言次数不少于9次的人数.
(3)已知A、F组发言的学生中都恰有1位女生,现从A组与F组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.

(1)求出抽取的该班人数,并补全直方图.
(2)该年级共有学生600人,请估计全年级在这天里发言次数不少于9次的人数.
(3)已知A、F组发言的学生中都恰有1位女生,现从A组与F组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率.
| 发言次数n | |
| A | 0≤n<3 |
| B | 3≤n<6 |
| C | 6≤n<9 |
| D | 9≤n<12 |
| E | 12≤n<15 |
| F | 15≤n<18 |
7.若⊙O的半径为4cm,点A到圆心O的距离为4.5cm,那么点A与⊙O的位置关系是( )
| A. | 点A在圆内 | B. | 点A在圆上 | C. | 点A在圆外 | D. | 不能确定 |
11.参加保险公司的医疗保险,住院治疗的病人享受分段报销,保险公司制定的报销细则如下表:
某人住院治疗后得到保险公司报销金额是1000元,那么此人住院的医疗费大约是2889元.
| 住院医疗费(元) | 报销率(%) |
| 不超过500元的部分 | 0 |
| 超过500~1000元的部分 | 30 |
| 超过1000~3000元的部分 | 45 |
| … |
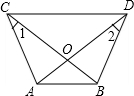 如图,已知AD与BC相交于点O,AC=BD,∠1=∠2.
如图,已知AD与BC相交于点O,AC=BD,∠1=∠2.