题目内容
如图1是抛物线形的拱桥,当水面在l时,拱顶离水面2米,水面宽4米.
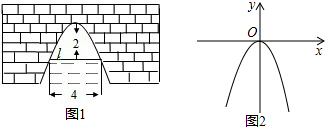
(1)借助图2的直角坐标系,求此抛物线的解析式;
(2)当水面下降1米时,求水面宽增加了多少米?

(1)借助图2的直角坐标系,求此抛物线的解析式;
(2)当水面下降1米时,求水面宽增加了多少米?
考点:二次函数的应用
专题:
分析:(1)根据建立的直角坐标系,设抛物线为y=ax2,把点(2,-2)代入求出解析式可解;
(2)利用(1)中所求解析式,进而将y=-3代入求出水面宽度,即可得出水面宽度增加的值.
(2)利用(1)中所求解析式,进而将y=-3代入求出水面宽度,即可得出水面宽度增加的值.
解答:解:(1)如图,建立直角坐标,(1分)
可设这条抛物线为y=ax2,
把点(2,-2)代入,得
-2=a×22,a=-
,
∴y=-
,
∴此抛物线的解析式为:y=-
x2;
(2)∵当水面下降1米时,
即当y=-3时,-3=-
x2,
解得:x=±
,
∴水面下降1m,水面宽度增加(2
-4)m.
可设这条抛物线为y=ax2,
把点(2,-2)代入,得
-2=a×22,a=-
| 1 |
| 2 |
∴y=-
| 1 |
| 2 |
∴此抛物线的解析式为:y=-
| 1 |
| 2 |
(2)∵当水面下降1米时,
即当y=-3时,-3=-
| 1 |
| 2 |
解得:x=±
| 6 |
∴水面下降1m,水面宽度增加(2
| 6 |
点评:此题主要考查了二次函数的应用,根据已知图象假设出解析式,进而求出是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
下列药品商标中是中心对称图形的是( )
A、 |
B、 |
C、 |
D、 |
下列各数:
,
,
,
,0,0.5,0.202002 …(相邻两个2之间0的个数逐次增加1个),其中是无理数的有( )
| 3 | 64 |
| 24 |
| 7 |
| π |
| 3 |
| 8 |
| A、2个 | B、3个 | C、4个 | D、5个 |
 如图,AB⊥a于B,DC⊥a于C,∠BMA=75°,∠DMC=45°,AM=DM.
如图,AB⊥a于B,DC⊥a于C,∠BMA=75°,∠DMC=45°,AM=DM. 如图,已知抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,8),若抛物线的对称轴为直线x=-1,且△ABC的面积为40.
如图,已知抛物线y=ax2+bx+c交x轴于A、B两点,交y轴于点C(0,8),若抛物线的对称轴为直线x=-1,且△ABC的面积为40. 已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且OE=OF.
已知:如图,AB是⊙O的弦,半径OC、OD分别交AB于点E、F,且OE=OF. 为了弘扬雷锋精神,某中学准备在校园内建造一座高2m的雷锋人体雕像,向全体师生征集设计方小琦同学查阅了有关资料,了解到黄金分割数常用于人体雕像的设计中.如图是小琦同学根据黄金分割数设计的雷锋人体雕像的方案,其中雷锋人体雕像下部的设计高度
为了弘扬雷锋精神,某中学准备在校园内建造一座高2m的雷锋人体雕像,向全体师生征集设计方小琦同学查阅了有关资料,了解到黄金分割数常用于人体雕像的设计中.如图是小琦同学根据黄金分割数设计的雷锋人体雕像的方案,其中雷锋人体雕像下部的设计高度 如图的方格纸中,每个小方格都是边长为1个单位的正方形,如图所示的阴影部分是由两个半径为1和一个半径为2的圆弧围成的图形.
如图的方格纸中,每个小方格都是边长为1个单位的正方形,如图所示的阴影部分是由两个半径为1和一个半径为2的圆弧围成的图形.