Question

18．如图，在矩形ABCD中，AB=6cm，AD=8cm，点P从点B出发，沿对角线BD向点D匀速运动，速度为4cm/s，过点P作PQ⊥BD交BC于点Q，以PQ为一边作正方形PQMN，使得点N落在射线PD上，点O从点D出发，沿DC向点C匀速运动，速度为3m/s，以O为圆心，0.8cm为半径作⊙O，点P与点O同时出发，设它们的运动时间为t（单位：s）（0＜t＜$\frac{8}{5}$）．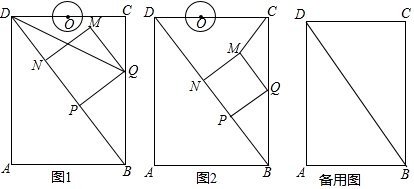

（1）如图1，连接DQ平分∠BDC时，t的值为1；
（2）如图2，连接CM，若△CMQ是以CQ为底的等腰三角形，求t的值；
（3）在运动过程中，当直线MN与⊙O相切时，求t的值．

Answer 1

分析 （1）根据速度和时间表示PB=4t，利用同角的三角函数列式为：tan∠DBC=$\frac{DC}{BC}$=$\frac{PQ}{PB}$，得PQ=3t；则BQ=5t，根据角平分线的性质得：CQ=PQ，列方程可得结果；
（2）如图2中，作MT⊥BC于T，由等腰三角形三线合一得：TQ=$\frac{1}{2}$（8-5t），证明△QTM∽△BCD，列比例式得$\frac{QM}{BD}=\frac{TQ}{BC}$，代入可得方程，解方程即可；
（3）由题意∠OEF=∠DEN=∠ADB，则sin∠OEF=sin∠DEN=sin∠ADB=3：5，
分两种情况：①若点O在正方形外MN与⊙O相切，如图3所示，根据同角的三角函数列式可得结果；
②若点O在正方形内MN与⊙O相切，如图4所示，同理列式：$\frac{10-7t}{3t-\frac{4}{3}}$=$\frac{3}{5}$，解出即可．

解答 解：（1）由题意得：PB=4t，
∵四边形ABCD是矩形，
∴∠C=90°
∵PQ⊥BC
∴∠BPQ=90°
∵BC=AD=8，CD=6
∴tan∠DBC=$\frac{DC}{BC}$=$\frac{PQ}{PB}$
∴$\frac{6}{8}$=$\frac{PQ}{4t}$
∴PQ=3t
由勾股定理得：BQ=5t
∴CQ=BC-BQ=8-5t，
∵DQ平分∠BDC，DC⊥BC，
∴CQ=PQ，
则8-5t=3t，
t=1；
故答案为：1；
（2）如图2中，作MT⊥BC于T，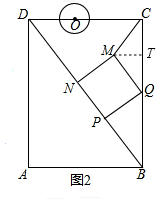
∵MC=MQ，MT⊥CQ，
∴TC=TQ，
由（1）可知TQ=$\frac{1}{2}$（8-5t），QM=PQ=3t，
∵四边形PQMN为正方形，
∴MQ∥PN，
∴∠MQT=∠DBC，
∴△QTM∽△BCD，
∴$\frac{QM}{BD}=\frac{TQ}{BC}$，
∴$\frac{3t}{10}$=$\frac{\frac{1}{2}（8-5t）}{8}$，
∴t=$\frac{40}{49}$（s）；
∴t=$\frac{40}{49}$s时，△CMQ是以CQ为底的等腰三角形；
（3）设MN与⊙O相切于点F，与CD交于点E，则OF=0.8，
由题意∠OEF=∠DEN=∠ADB，
∴sin∠OEF=sin∠DEN=sin∠ADB=3：5，
∴$\frac{OF}{OE}=\frac{3}{5}$，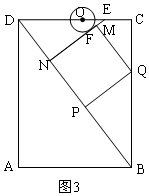
∴$\frac{0.8}{OE}=\frac{3}{5}$，
∴OE=$\frac{4}{3}$，
①若点O在正方形外MN与⊙O相切，如图3所示，
∵OD=3t，
∴DE=3t+$\frac{4}{3}$，
∵BP=4t，NP=PQ=3t，
∴DN=10-7t，
∴$\frac{10-7t}{3t+\frac{4}{3}}$=$\frac{3}{5}$，
∴t=$\frac{23}{22}$；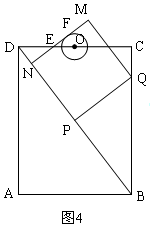

②若点O在正方形内MN与⊙O相切，如图4所示，
∵OD=3t∴DE=3t-$\frac{4}{3}$，
∵BP=4t，NP=PQ=3t，
∴DN=10-7t，
∴$\frac{10-7t}{3t-\frac{4}{3}}$=$\frac{3}{5}$，
∴t=$\frac{27}{22}$，
综上所述，当直线MN与⊙O相切时，t的值是$\frac{23}{22}$s或$\frac{27}{22}$s．

点评 本题是圆的综合题，考查了图形运动、相似三角形的性质和判定、解直角三角形，熟练掌握性质定理是解题的关键，尤其是运用同角的三角函数列比例式比相似要简单，因此要经常运用．