题目内容
8. 已知如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,∠GMN+∠HNM=90°,试问:AB∥CD吗?请说明理由.
已知如图,AB、CD被EF所截,MG平分∠BMN,NH平分∠DNM,∠GMN+∠HNM=90°,试问:AB∥CD吗?请说明理由.
分析 先利用角平分线定义得到∠1=$\frac{1}{2}$∠BMN,∠2=$\frac{1}{2}$∠DNM,则∠1+∠2=$\frac{1}{2}$(∠BMN+∠DNM),再利用∠1+∠2=90°可得∠BMN+∠DNM=180°,然后根据内错角相等,两直线平行可判断AB∥CD.
解答 解:AB∥CD.理由如下: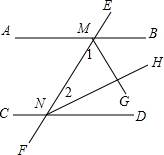
∵MG平分∠BMN,NH平分∠DNM,
∴∠1=$\frac{1}{2}$∠BMN,∠2=$\frac{1}{2}$∠DNM,
∴∠1+∠2=$\frac{1}{2}$(∠BMN+∠DNM),
∵∠1+∠2=90°,
∴∠BMN+∠DNM=180°,
∴AB∥CD.
点评 本题考了平行线的判定:同位角相等,两直线平行:内错角相等,两直线平行;内错角相等,两直线平行.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
16.我国自主研制的“天河二号”超级计算机,其浮点运算速度高达每秒33.86千万亿次.33.86千万用科学记数法表示为( )
| A. | 0.3386×109 | B. | 3.386×108 | C. | 3.386×109 | D. | 33.86×107 |
3.已知实数x,y满足$\sqrt{x-1}$+|y+3|=0,则3x+2y的值为( )
| A. | -2 | B. | 3 | C. | $\frac{25}{8}$ | D. | -4 |
 某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃.
某地连续统计了10天日最高气温,并绘制成如图所示的扇形统计图.计算这10天日最高气温的平均值为34.3℃. 已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.
已知:如图,在△ABC中,∠CAB=2α,且0°<α<30°,AP平分∠CAB.若α=21°,∠ABC=32°,且AP交BC于点P,试探究线段AB,AC与PB之间的数量关系,并对你的结论加以证明.